Question Number 70980 by ~ À ® @ 237 ~ last updated on 10/Oct/19
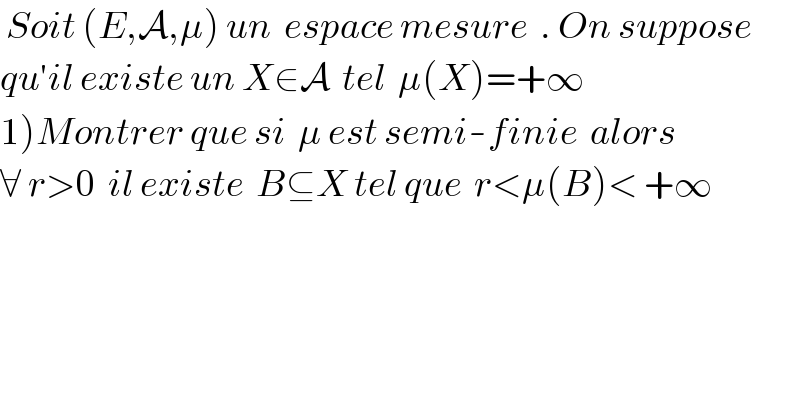
$$\:{Soit}\:\left({E},\mathcal{A},\mu\right)\:{un}\:\:{espace}\:{mesure}\:\:.\:{On}\:{suppose} \\ $$$${qu}'{il}\:{existe}\:{un}\:{X}\in\mathcal{A}\:\:{tel}\:\:\mu\left({X}\right)=+\infty \\ $$$$\left.\mathrm{1}\right){Montrer}\:{que}\:{si}\:\:\mu\:{est}\:{semi}-{finie}\:\:{alors} \\ $$$$\forall\:{r}>\mathrm{0}\:\:{il}\:{existe}\:\:{B}\subseteq{X}\:{tel}\:{que}\:\:{r}<\mu\left({B}\right)<\:+\infty \\ $$$$ \\ $$
