Question Number 73468 by mathocean1 last updated on 12/Nov/19

$$\mathrm{soit}\:\mathrm{le}\:\mathrm{systeme}\:\mathrm{suivant} \\ $$$$\begin{cases}{\mathrm{2s}+\mathrm{4c}+\mathrm{3t}=\mathrm{700}}\\{\mathrm{3s}+\mathrm{2c}+\mathrm{2t}=\mathrm{500}}\end{cases} \\ $$$$\:\:\mathrm{8s}+\mathrm{7c}+\mathrm{8t}=…?… \\ $$$$\mathrm{comment}\:\mathrm{determiner}\:\mathrm{le}\:\mathrm{resultat}\:…?…\: \\ $$$$\mathrm{de}\:\mathrm{la}\:\mathrm{3}^{\mathrm{e}} \mathrm{equation}\:? \\ $$
Answered by MJS last updated on 13/Nov/19
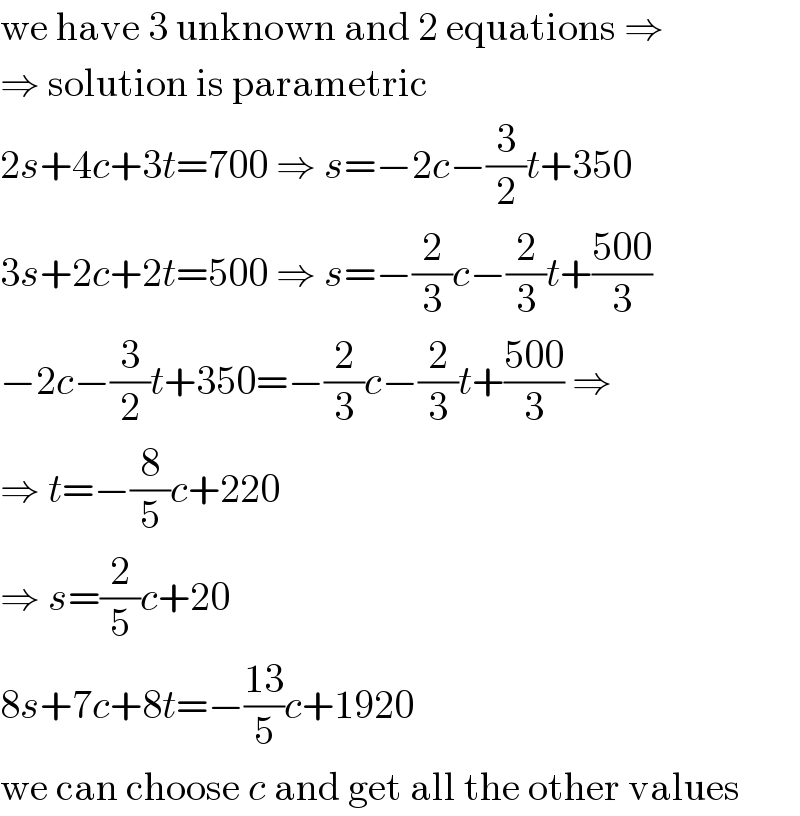
$$\mathrm{we}\:\mathrm{have}\:\mathrm{3}\:\mathrm{unknown}\:\mathrm{and}\:\mathrm{2}\:\mathrm{equations}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{solution}\:\mathrm{is}\:\mathrm{parametric} \\ $$$$\mathrm{2}{s}+\mathrm{4}{c}+\mathrm{3}{t}=\mathrm{700}\:\Rightarrow\:{s}=−\mathrm{2}{c}−\frac{\mathrm{3}}{\mathrm{2}}{t}+\mathrm{350} \\ $$$$\mathrm{3}{s}+\mathrm{2}{c}+\mathrm{2}{t}=\mathrm{500}\:\Rightarrow\:{s}=−\frac{\mathrm{2}}{\mathrm{3}}{c}−\frac{\mathrm{2}}{\mathrm{3}}{t}+\frac{\mathrm{500}}{\mathrm{3}} \\ $$$$−\mathrm{2}{c}−\frac{\mathrm{3}}{\mathrm{2}}{t}+\mathrm{350}=−\frac{\mathrm{2}}{\mathrm{3}}{c}−\frac{\mathrm{2}}{\mathrm{3}}{t}+\frac{\mathrm{500}}{\mathrm{3}}\:\Rightarrow \\ $$$$\Rightarrow\:{t}=−\frac{\mathrm{8}}{\mathrm{5}}{c}+\mathrm{220} \\ $$$$\Rightarrow\:{s}=\frac{\mathrm{2}}{\mathrm{5}}{c}+\mathrm{20} \\ $$$$\mathrm{8}{s}+\mathrm{7}{c}+\mathrm{8}{t}=−\frac{\mathrm{13}}{\mathrm{5}}{c}+\mathrm{1920} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{choose}\:{c}\:\mathrm{and}\:\mathrm{get}\:\mathrm{all}\:\mathrm{the}\:\mathrm{other}\:\mathrm{values} \\ $$
