Question Number 1831 by Filup last updated on 10/Oct/15
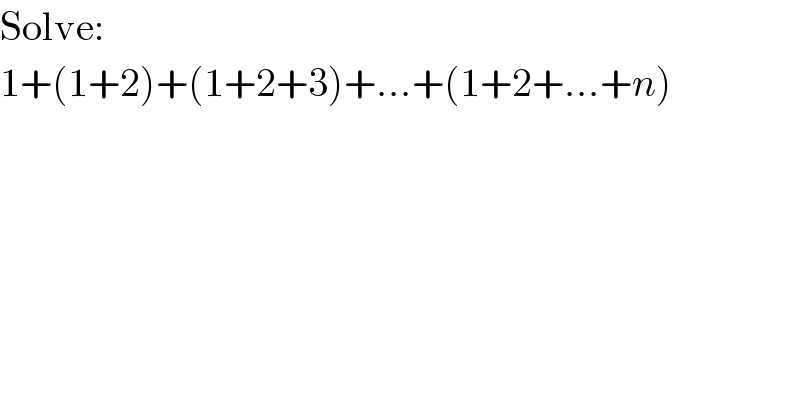
$$\mathrm{Solve}: \\ $$$$\mathrm{1}+\left(\mathrm{1}+\mathrm{2}\right)+\left(\mathrm{1}+\mathrm{2}+\mathrm{3}\right)+…+\left(\mathrm{1}+\mathrm{2}+…+{n}\right) \\ $$
Answered by Rasheed Soomro last updated on 10/Oct/15
![1+(1+2)+(1+2+3)+...+(1+2+...+n) =(1/2)(1)(1+1)+(1/2)(2)(2+1)+...+(1/2)n(n+1) =(1/2){1.2+2.3+3.4+...n(n+1)} =(1/2)Σn(n+1)=(1/2)Σ(n^2 +n) =(1/2){Σ n^2 +Σ n} =(1/2){((n(n+1)(2n+1))/6)+((n(n+1))/2)} =(1/2){((n(n+1))/2) [((2n+1)/3)+1]} =(1/2){((n(n+1)(n+2))/3)} =((n(n+1)(n+2))/6)](https://www.tinkutara.com/question/Q1832.png)
$$\mathrm{1}+\left(\mathrm{1}+\mathrm{2}\right)+\left(\mathrm{1}+\mathrm{2}+\mathrm{3}\right)+…+\left(\mathrm{1}+\mathrm{2}+…+{n}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\right)\left(\mathrm{2}+\mathrm{1}\right)+…+\frac{\mathrm{1}}{\mathrm{2}}{n}\left({n}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{1}.\mathrm{2}+\mathrm{2}.\mathrm{3}+\mathrm{3}.\mathrm{4}+…{n}\left({n}+\mathrm{1}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Sigma{n}\left({n}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\Sigma\left({n}^{\mathrm{2}} +{n}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\Sigma\:{n}^{\mathrm{2}} +\Sigma\:{n}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:\left[\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{3}}+\mathrm{1}\right]\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{3}}\right\} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{6}} \\ $$
