Question Number 1961 by alib last updated on 26/Oct/15
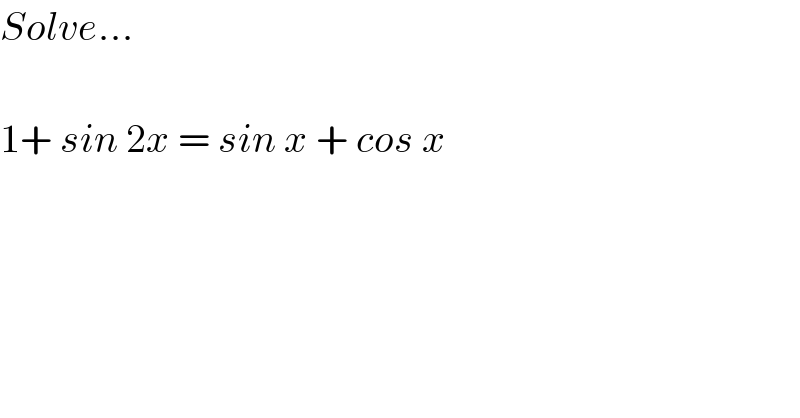
$${Solve}… \\ $$$$ \\ $$$$\mathrm{1}+\:{sin}\:\mathrm{2}{x}\:=\:{sin}\:{x}\:+\:{cos}\:{x} \\ $$
Answered by Rasheed Soomro last updated on 26/Oct/15

$$\mathrm{1}+\:{sin}\:\mathrm{2}{x}\:=\:{sin}\:{x}\:+\:{cos}\:{x} \\ $$$$\mathrm{1}+\mathrm{2}{sin}\:{x}\:{cos}\:{x}−{sin}\:{x}\:−{cos}\:{x}=\mathrm{0} \\ $$$${sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}+\mathrm{2}{sin}\:{x}\:{cos}\:{x}\:−\left({sin}\:{x}+{cos}\:{x}\right)=\mathrm{0}\: \\ $$$$\left({sin}\:{x}\:+{cos}\:{x}\right)^{\mathrm{2}} −\left({sin}\:{x}+{cos}\:{x}\right)=\mathrm{0} \\ $$$$\left({sin}\:{x}+{cos}\:{x}\right)\left({sin}\:{x}+{cos}\:{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${sin}\:{x}\:+\:{cos}\:{x}\:=\:\mathrm{0}\:\mid\:{sin}\:{x}+{cos}\:{x}−\mathrm{1}=\mathrm{0} \\ $$$${sin}\:{x}\:+\:{cos}\:{x}\:=\:\mathrm{0}\:\mid\:{sin}\:{x}\:+{cos}\:{x}=\mathrm{1} \\ $$$${sin}\:{x}=−{cos}\:{x}\:\:\:\:\:\:\:\mid\:{sin}\:{x}=\mathrm{1}−{cos}\:{x} \\ $$$${sin}^{\mathrm{2}} {x}={cos}^{\mathrm{2}} {x}\:\:\:\:\:\:\:\:\:\mid{sin}^{\mathrm{2}} {x}=\mathrm{1}+{cos}^{\mathrm{2}} {x}−\mathrm{2}\:{cos}\:{x} \\ $$$${sin}^{\mathrm{2}} {x}=\mathrm{1}−{sin}^{\mathrm{2}} {x}\:\:\:\mid\:\mathrm{1}−{cos}^{\mathrm{2}} {x}=\mathrm{1}+{cos}^{\mathrm{2}} {x}−\mathrm{2}\:{cos}\:{x} \\ $$$${sin}^{\mathrm{2}} {x}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:{cos}^{\mathrm{2}} {x}−{cos}\:{x}=\mathrm{0} \\ $$$${x}={sin}^{−\mathrm{1}} \left(\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\:\:\:\:\:\:\mid\:{cos}\:{x}\left({cos}\:{x}−\mathrm{1}\right)=\mathrm{0}\Rightarrow{cos}\:{x}=\mathrm{0}\:\vee\:{cos}\:{x}=\mathrm{1} \\ $$$${x}=\frac{\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}},\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}}\:{in}\:{the}\:{interval}\:\left(\mathrm{0},\mathrm{2}\pi\right)\:\mid\:{x}=\frac{\pi}{\mathrm{2}},\frac{\mathrm{3}\pi}{\mathrm{2}},\mathrm{0}\:{in}\:\left(\mathrm{0},\mathrm{2}\pi\right) \\ $$$${Extraneous}\:{roots}\:{may}\:{be}\:{inluded}. \\ $$
