Menu Close

Solve-1-x-2-dy-dx-xy-xp-

Tinku Tara 0 Comments
Pin




Question Number 6991 by Tawakalitu. last updated on 05/Aug/16
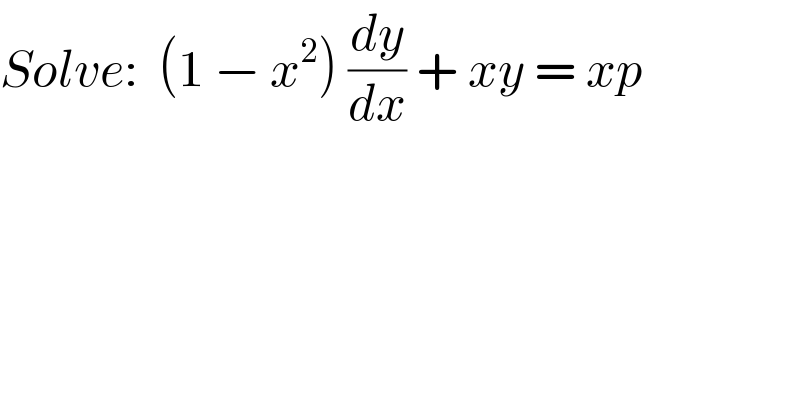
Solve: (1 − x^2 ) (dy/dx) + xy = xp
$${Solve}:\:\:\left(\mathrm{1}\:−\:{x}^{\mathrm{2}} \right)\:\frac{{dy}}{{dx}}\:+\:{xy}\:=\:{xp} \\ $$$$ \\ $$$$ \\ $$
Answered by Yozzii last updated on 05/Aug/16
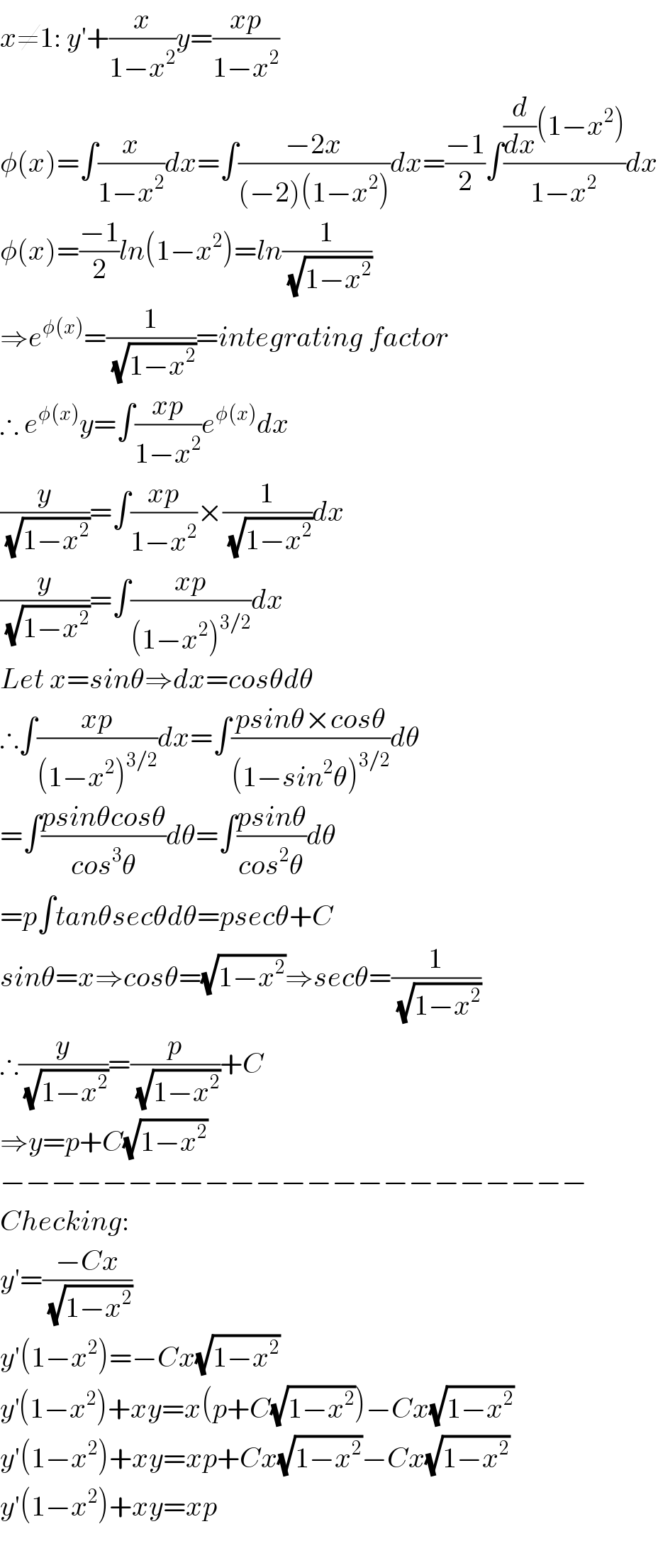
x≠1: y′+(x/(1−x^2 ))y=((xp)/(1−x^2 )) φ(x)=∫(x/(1−x^2 ))dx=∫((−2x)/((−2)(1−x^2 )))dx=((−1)/2)∫(((d/dx)(1−x^2 ))/(1−x^2 ))dx φ(x)=((−1)/2)ln(1−x^2 )=ln(1/( (√(1−x^2 )))) ⇒e^(φ(x)) =(1/( (√(1−x^2 ))))=integrating factor ∴ e^(φ(x)) y=∫((xp)/(1−x^2 ))e^(φ(x)) dx (y/( (√(1−x^2 ))))=∫((xp)/(1−x^2 ))×(1/( (√(1−x^2 ))))dx (y/( (√(1−x^2 ))))=∫((xp)/((1−x^2 )^(3/2) ))dx Let x=sinθ⇒dx=cosθdθ ∴∫((xp)/((1−x^2 )^(3/2) ))dx=∫((psinθ×cosθ)/((1−sin^2 θ)^(3/2) ))dθ =∫((psinθcosθ)/(cos^3 θ))dθ=∫((psinθ)/(cos^2 θ))dθ =p∫tanθsecθdθ=psecθ+C sinθ=x⇒cosθ=(√(1−x^2 ))⇒secθ=(1/( (√(1−x^2 )))) ∴(y/( (√(1−x^2 ))))=(p/( (√(1−x^2 ))))+C ⇒y=p+C(√(1−x^2 )) −−−−−−−−−−−−−−−−−−−−−−− Checking: y′=((−Cx)/( (√(1−x^2 )))) y′(1−x^2 )=−Cx(√(1−x^2 )) y^′ (1−x^2 )+xy=x(p+C(√(1−x^2 )))−Cx(√(1−x^2 )) y′(1−x^2 )+xy=xp+Cx(√(1−x^2 ))−Cx(√(1−x^2 )) y′(1−x^2 )+xy=xp
$${x}\neq\mathrm{1}:\:{y}'+\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }{y}=\frac{{xp}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\phi\left({x}\right)=\int\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\int\frac{−\mathrm{2}{x}}{\left(−\mathrm{2}\right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{dx}=\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{\frac{{d}}{{dx}}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$\phi\left({x}\right)=\frac{−\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)={ln}\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow{e}^{\phi\left({x}\right)} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}={integrating}\:{factor} \\ $$$$\therefore\:{e}^{\phi\left({x}\right)} {y}=\int\frac{{xp}}{\mathrm{1}−{x}^{\mathrm{2}} }{e}^{\phi\left({x}\right)} {dx} \\ $$$$\frac{{y}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\int\frac{{xp}}{\mathrm{1}−{x}^{\mathrm{2}} }×\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$\frac{{y}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\int\frac{{xp}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }{dx} \\ $$$${Let}\:{x}={sin}\theta\Rightarrow{dx}={cos}\theta{d}\theta \\ $$$$\therefore\int\frac{{xp}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }{dx}=\int\frac{{psin}\theta×{cos}\theta}{\left(\mathrm{1}−{sin}^{\mathrm{2}} \theta\right)^{\mathrm{3}/\mathrm{2}} }{d}\theta \\ $$$$=\int\frac{{psin}\theta{cos}\theta}{{cos}^{\mathrm{3}} \theta}{d}\theta=\int\frac{{psin}\theta}{{cos}^{\mathrm{2}} \theta}{d}\theta \\ $$$$={p}\int{tan}\theta{sec}\theta{d}\theta={psec}\theta+{C} \\ $$$${sin}\theta={x}\Rightarrow{cos}\theta=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\Rightarrow{sec}\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\therefore\frac{{y}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\frac{{p}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+{C} \\ $$$$\Rightarrow{y}={p}+{C}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Checking}: \\ $$$${y}'=\frac{−{Cx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${y}'\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=−{Cx}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${y}^{'} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)+{xy}={x}\left({p}+{C}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)−{Cx}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${y}'\left(\mathrm{1}−{x}^{\mathrm{2}} \right)+{xy}={xp}+{Cx}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−{Cx}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${y}'\left(\mathrm{1}−{x}^{\mathrm{2}} \right)+{xy}={xp} \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 05/Aug/16
Great. thanks so much.
$${Great}.\:{thanks}\:{so}\:{much}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *