Question Number 185 by 123456 last updated on 25/Jan/15

$$\mathrm{solve}\:\mathrm{10x}\equiv\mathrm{25}\left(\mathrm{mod}\:\mathrm{15}\right) \\ $$
Answered by mreddy last updated on 14/Dec/14
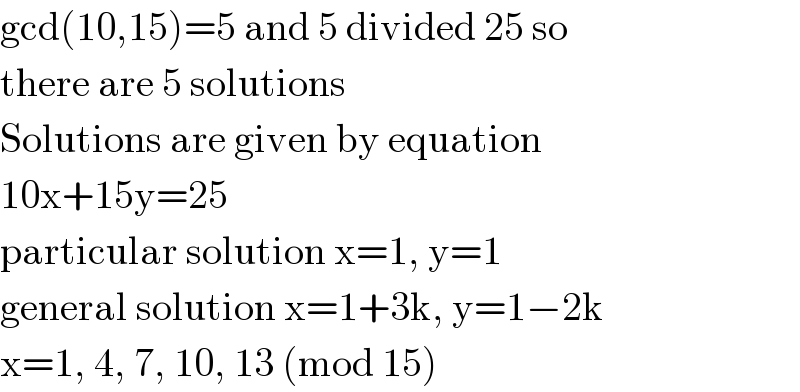
$$\mathrm{gcd}\left(\mathrm{10},\mathrm{15}\right)=\mathrm{5}\:\mathrm{and}\:\mathrm{5}\:\mathrm{divided}\:\mathrm{25}\:\mathrm{so}\: \\ $$$$\mathrm{there}\:\mathrm{are}\:\mathrm{5}\:\mathrm{solutions} \\ $$$$\mathrm{Solutions}\:\mathrm{are}\:\mathrm{given}\:\mathrm{by}\:\mathrm{equation} \\ $$$$\mathrm{10x}+\mathrm{15y}=\mathrm{25} \\ $$$$\mathrm{particular}\:\mathrm{solution}\:\mathrm{x}=\mathrm{1},\:\mathrm{y}=\mathrm{1} \\ $$$$\mathrm{general}\:\mathrm{solution}\:\mathrm{x}=\mathrm{1}+\mathrm{3k},\:\mathrm{y}=\mathrm{1}−\mathrm{2k} \\ $$$$\mathrm{x}=\mathrm{1},\:\mathrm{4},\:\mathrm{7},\:\mathrm{10},\:\mathrm{13}\:\left(\mathrm{mod}\:\mathrm{15}\right) \\ $$
