solve-2-x-4-x-8-x-

Question Number 138096 by mr W last updated on 10/Apr/21

$${solve} \\ $$$$\mathrm{2}^{{x}} +\mathrm{4}^{{x}} =\mathrm{8}^{{x}} \\ $$

Commented by MJS_new last updated on 10/Apr/21

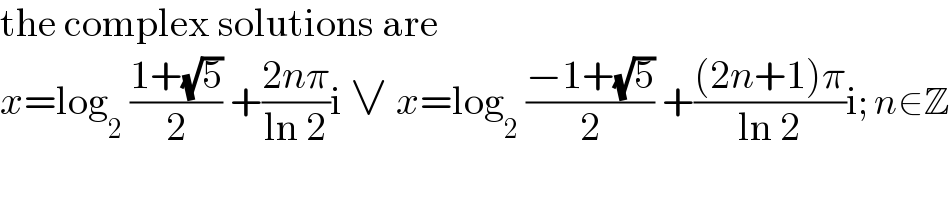
the complex solutions are x=log_2 ((1+(√5))/2) +((2nπ)/(ln 2))i ∨ x=log_2 ((−1+(√5))/2) +(((2n+1)π)/(ln 2))i; n∈Z

$$\mathrm{the}\:\mathrm{complex}\:\mathrm{solutions}\:\mathrm{are} \\ $$$${x}=\mathrm{log}_{\mathrm{2}} \:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:+\frac{\mathrm{2}{n}\pi}{\mathrm{ln}\:\mathrm{2}}\mathrm{i}\:\vee\:{x}=\mathrm{log}_{\mathrm{2}} \:\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:+\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{ln}\:\mathrm{2}}\mathrm{i};\:{n}\in\mathbb{Z} \\ $$

Answered by liberty last updated on 10/Apr/21

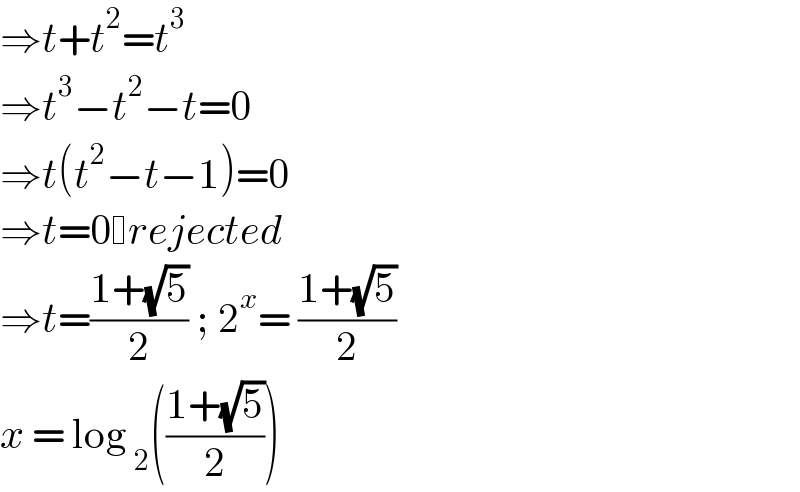
⇒t+t^2 =t^3 ⇒t^3 −t^2 −t=0 ⇒t(t^2 −t−1)=0 ⇒t=0 rejected ⇒t=((1+(√5))/2) ; 2^x = ((1+(√5))/2) x = log _2 (((1+(√5))/2))

$$\Rightarrow{t}+{t}^{\mathrm{2}} ={t}^{\mathrm{3}} \\ $$$$\Rightarrow{t}^{\mathrm{3}} −{t}^{\mathrm{2}} −{t}=\mathrm{0} \\ $$$$\Rightarrow{t}\left({t}^{\mathrm{2}} −{t}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{0} {rejected} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:;\:\mathrm{2}^{{x}} =\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}\:=\:\mathrm{log}\:_{\mathrm{2}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$

Commented by mr W last updated on 10/Apr/21

$${nice}! \\ $$

Commented by liberty last updated on 10/Apr/21

��

Commented by chengulapetrom last updated on 10/Apr/21

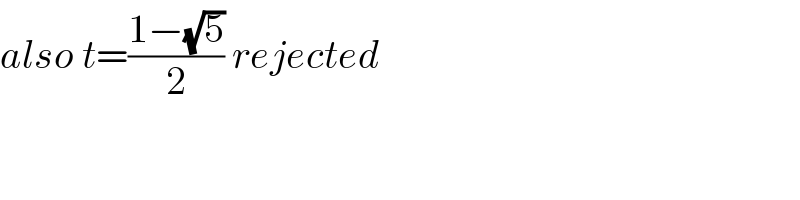
$${also}\:{t}=\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:{rejected} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply