Solve-2x-x-7-2-x-3-2-0-

Question Number 8071 by marcusvsoliveira last updated on 29/Sep/16

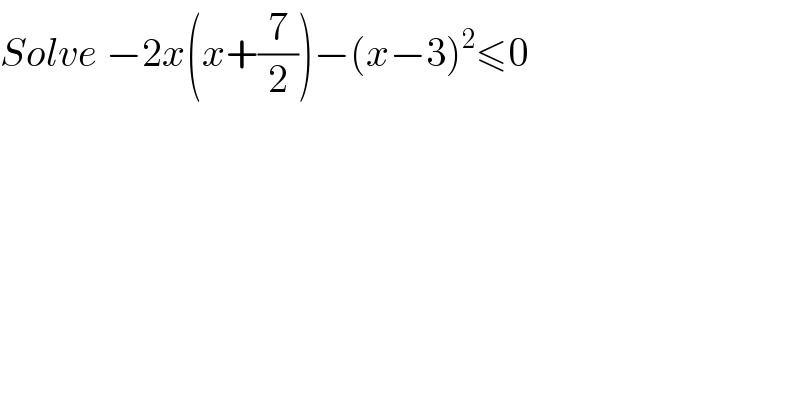
$${Solve}\:−\mathrm{2}{x}\left({x}+\frac{\mathrm{7}}{\mathrm{2}}\right)−\left({x}−\mathrm{3}\right)^{\mathrm{2}} \leqslant\mathrm{0} \\ $$

Commented by FilupSmith last updated on 29/Sep/16

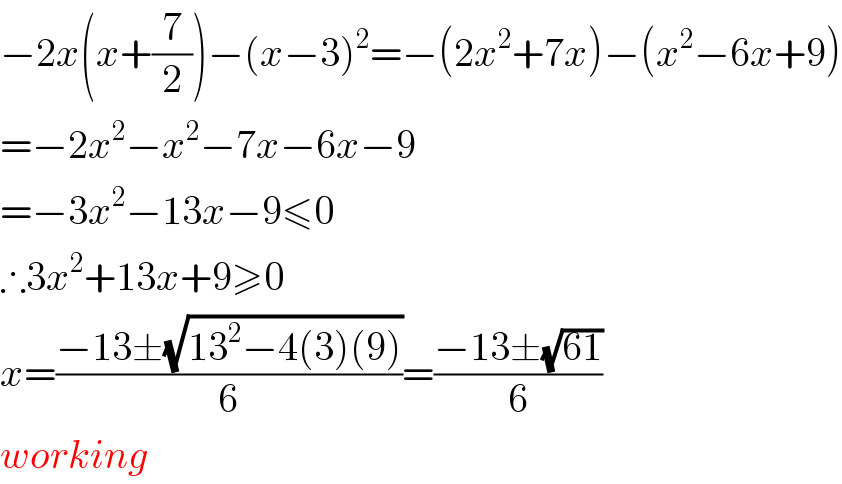
−2x(x+(7/2))−(x−3)^2 =−(2x^2 +7x)−(x^2 −6x+9) =−2x^2 −x^2 −7x−6x−9 =−3x^2 −13x−9≤0 ∴3x^2 +13x+9≥0 x=((−13±(√(13^2 −4(3)(9))))/6)=((−13±(√(61)))/6) working

$$−\mathrm{2}{x}\left({x}+\frac{\mathrm{7}}{\mathrm{2}}\right)−\left({x}−\mathrm{3}\right)^{\mathrm{2}} =−\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{7}{x}\right)−\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}\right) \\ $$$$=−\mathrm{2}{x}^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{6}{x}−\mathrm{9} \\ $$$$=−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{13}{x}−\mathrm{9}\leqslant\mathrm{0} \\ $$$$\therefore\mathrm{3}{x}^{\mathrm{2}} +\mathrm{13}{x}+\mathrm{9}\geqslant\mathrm{0} \\ $$$${x}=\frac{−\mathrm{13}\pm\sqrt{\mathrm{13}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{3}\right)\left(\mathrm{9}\right)}}{\mathrm{6}}=\frac{−\mathrm{13}\pm\sqrt{\mathrm{61}}}{\mathrm{6}} \\ $$$${working} \\ $$

Commented by marcusvsoliveira last updated on 29/Sep/16

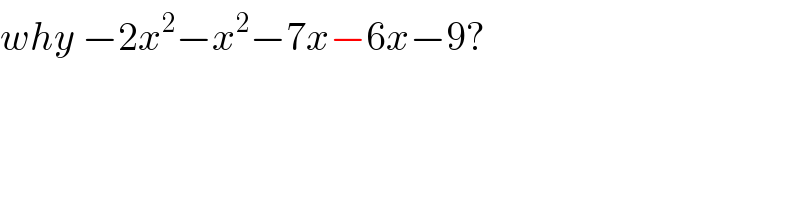
$${why}\:−\mathrm{2}{x}^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{6}{x}−\mathrm{9}? \\ $$

Answered by prakash jain last updated on 29/Sep/16

−2x(x+(7/2))−(x−3)^2 ≤0 −2x^2 −7x−x^2 +6x−9≤0 −3x^2 −x−9≤0 −3x^2 −x−9≤0 root are ((1±(√(1−27×4)))/(−6)) ⇒no real root as the quadratic has no real roots it takes the same as coefficient of x^2 for x∈R. −3x^2 −x−9≤0 for x∈R Solution set R

$$−\mathrm{2}{x}\left({x}+\frac{\mathrm{7}}{\mathrm{2}}\right)−\left({x}−\mathrm{3}\right)^{\mathrm{2}} \leqslant\mathrm{0} \\ $$$$−\mathrm{2}{x}^{\mathrm{2}} −\mathrm{7}{x}−{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{9}\leqslant\mathrm{0} \\ $$$$−\mathrm{3}{x}^{\mathrm{2}} −{x}−\mathrm{9}\leqslant\mathrm{0} \\ $$$$−\mathrm{3}{x}^{\mathrm{2}} −{x}−\mathrm{9}\leqslant\mathrm{0} \\ $$$${root}\:{are}\:\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{27}×\mathrm{4}}}{−\mathrm{6}}\:\Rightarrow{no}\:{real}\:{root} \\ $$$$\mathrm{as}\:\mathrm{the}\:\mathrm{quadratic}\:\mathrm{has}\:\mathrm{no}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{it} \\ $$$$\mathrm{takes}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{\mathrm{2}} \:\mathrm{for}\:{x}\in\mathbb{R}. \\ $$$$−\mathrm{3}{x}^{\mathrm{2}} −{x}−\mathrm{9}\leqslant\mathrm{0}\:\mathrm{for}\:{x}\in\mathbb{R} \\ $$$$\mathrm{Solution}\:\mathrm{set}\:\mathbb{R} \\ $$

Commented by FilupSmith last updated on 30/Sep/16

I made a silly error. no wonder i couldnt figure it out

$$\mathrm{I}\:\mathrm{made}\:\mathrm{a}\:\mathrm{silly}\:\mathrm{error}.\:\mathrm{no}\:\mathrm{wonder}\:\mathrm{i}\:\mathrm{couldnt} \\ $$$$\mathrm{figure}\:\mathrm{it}\:\mathrm{out} \\ $$

Facebook Tweet Pin

Solve-2x-x-7-2-x-3-2-0-

Leave a Reply Cancel reply