Question Number 137103 by Boucatchou last updated on 29/Mar/21
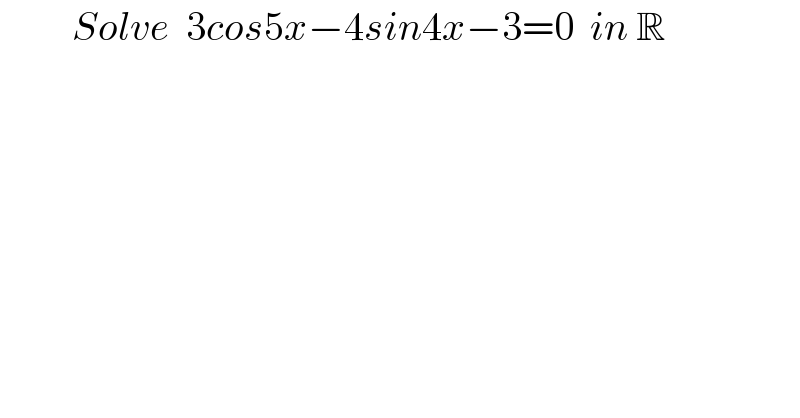
$$\:\:\:\:\:\:\:\:\:{Solve}\:\:\mathrm{3}{cos}\mathrm{5}{x}−\mathrm{4}{sin}\mathrm{4}{x}−\mathrm{3}=\mathrm{0}\:\:{in}\:\mathbb{R} \\ $$
Answered by MJS_new last updated on 30/Mar/21
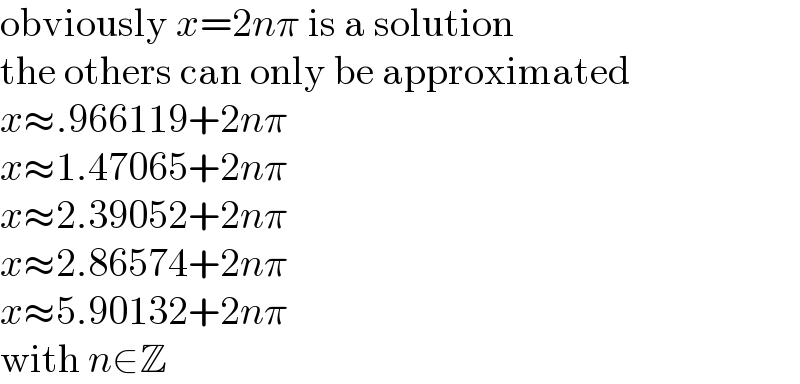
$$\mathrm{obviously}\:{x}=\mathrm{2}{n}\pi\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$$$\mathrm{the}\:\mathrm{others}\:\mathrm{can}\:\mathrm{only}\:\mathrm{be}\:\mathrm{approximated} \\ $$$${x}\approx.\mathrm{966119}+\mathrm{2}{n}\pi \\ $$$${x}\approx\mathrm{1}.\mathrm{47065}+\mathrm{2}{n}\pi \\ $$$${x}\approx\mathrm{2}.\mathrm{39052}+\mathrm{2}{n}\pi \\ $$$${x}\approx\mathrm{2}.\mathrm{86574}+\mathrm{2}{n}\pi \\ $$$${x}\approx\mathrm{5}.\mathrm{90132}+\mathrm{2}{n}\pi \\ $$$$\mathrm{with}\:{n}\in\mathbb{Z} \\ $$
