Menu Close

solve-4x-2-4x-1-y-12x-6-y-8x-3-1-12x-2-16y-6x-

Tinku Tara 0 Comments
Pin




Question Number 77803 by aliesam last updated on 10/Jan/20
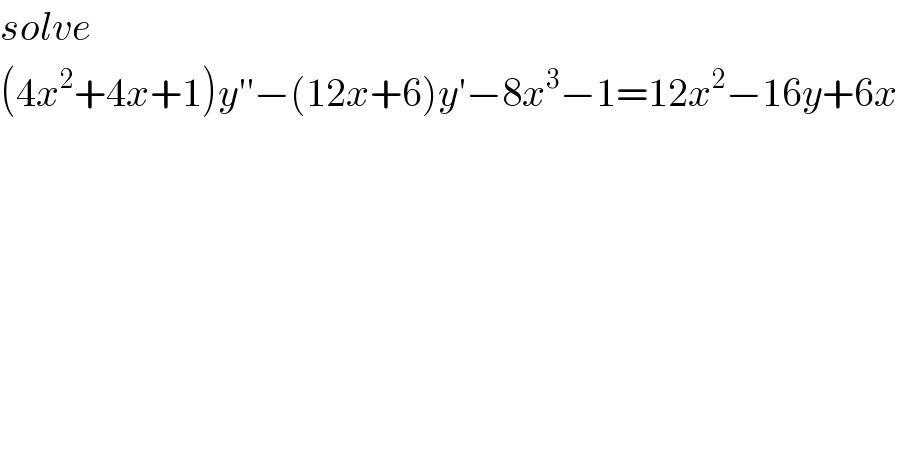
solve (4x^2 +4x+1)y′′−(12x+6)y′−8x^3 −1=12x^2 −16y+6x
$${solve} \\ $$$$\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}\right){y}''−\left(\mathrm{12}{x}+\mathrm{6}\right){y}'−\mathrm{8}{x}^{\mathrm{3}} −\mathrm{1}=\mathrm{12}{x}^{\mathrm{2}} −\mathrm{16}{y}+\mathrm{6}{x} \\ $$
Answered by mind is power last updated on 11/Jan/20
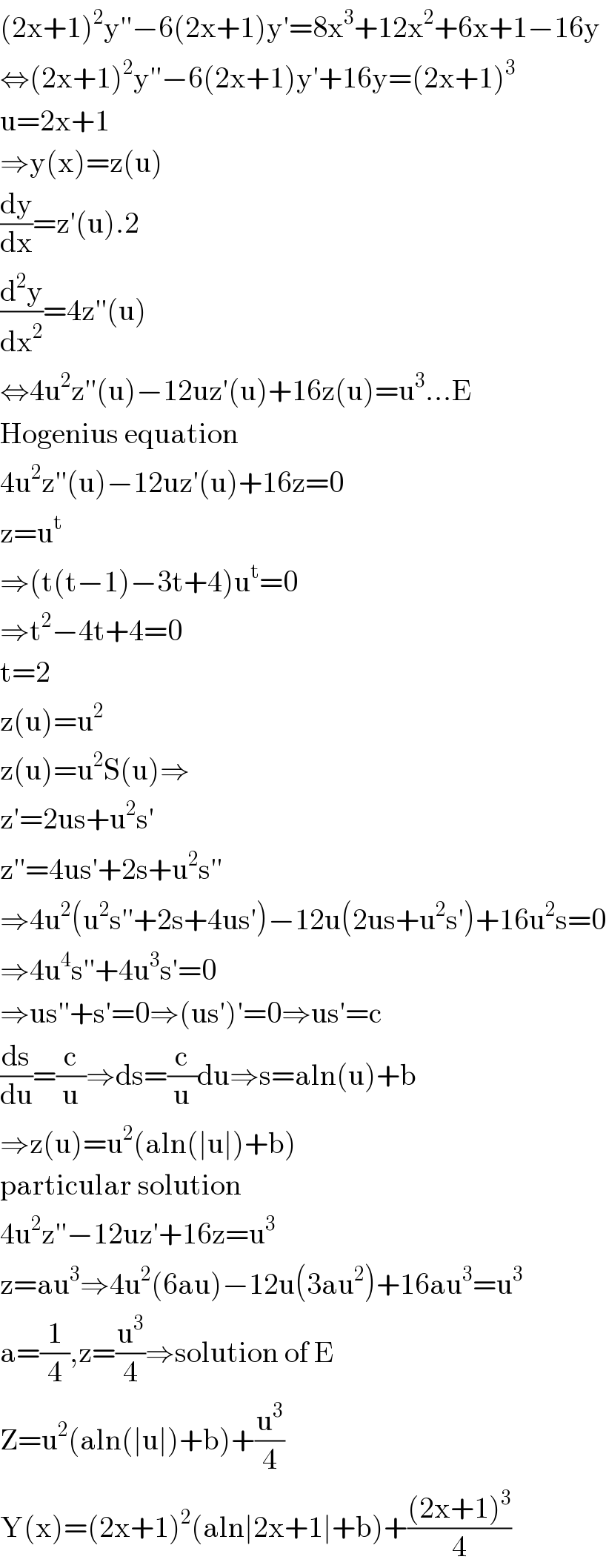
(2x+1)^2 y′′−6(2x+1)y′=8x^3 +12x^2 +6x+1−16y ⇔(2x+1)^2 y′′−6(2x+1)y′+16y=(2x+1)^3 u=2x+1 ⇒y(x)=z(u) (dy/dx)=z′(u).2 (d^2 y/dx^2 )=4z′′(u) ⇔4u^2 z′′(u)−12uz′(u)+16z(u)=u^3 ...E Hogenius equation 4u^2 z′′(u)−12uz′(u)+16z=0 z=u^t ⇒(t(t−1)−3t+4)u^t =0 ⇒t^2 −4t+4=0 t=2 z(u)=u^2 z(u)=u^2 S(u)⇒ z′=2us+u^2 s′ z′′=4us′+2s+u^2 s′^′ ⇒4u^2 (u^2 s′′+2s+4us′)−12u(2us+u^2 s′)+16u^2 s=0 ⇒4u^4 s′′+4u^3 s′=0 ⇒us′′+s′=0⇒(us′)′=0⇒us′=c (ds/du)=(c/u)⇒ds=(c/u)du⇒s=aln(u)+b ⇒z(u)=u^2 (aln(∣u∣)+b) particular solution 4u^2 z′′−12uz′+16z=u^3 z=au^3 ⇒4u^2 (6au)−12u(3au^2 )+16au^3 =u^3 a=(1/4),z=(u^3 /4)⇒solution of E Z=u^2 (aln(∣u∣)+b)+(u^3 /4) Y(x)=(2x+1)^2 (aln∣2x+1∣+b)+(((2x+1)^3 )/4)
$$\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{y}''−\mathrm{6}\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{y}'=\mathrm{8x}^{\mathrm{3}} +\mathrm{12x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{1}−\mathrm{16y} \\ $$$$\Leftrightarrow\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{y}''−\mathrm{6}\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{y}'+\mathrm{16y}=\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\mathrm{u}=\mathrm{2x}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\mathrm{z}\left(\mathrm{u}\right) \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{z}'\left(\mathrm{u}\right).\mathrm{2} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }=\mathrm{4z}''\left(\mathrm{u}\right) \\ $$$$\Leftrightarrow\mathrm{4u}^{\mathrm{2}} \mathrm{z}''\left(\mathrm{u}\right)−\mathrm{12uz}'\left(\mathrm{u}\right)+\mathrm{16z}\left(\mathrm{u}\right)=\mathrm{u}^{\mathrm{3}} …\mathrm{E} \\ $$$$\mathrm{Hogenius}\:\mathrm{equation} \\ $$$$\mathrm{4u}^{\mathrm{2}} \mathrm{z}''\left(\mathrm{u}\right)−\mathrm{12uz}'\left(\mathrm{u}\right)+\mathrm{16z}=\mathrm{0} \\ $$$$\mathrm{z}=\mathrm{u}^{\mathrm{t}} \\ $$$$\Rightarrow\left(\mathrm{t}\left(\mathrm{t}−\mathrm{1}\right)−\mathrm{3t}+\mathrm{4}\right)\mathrm{u}^{\mathrm{t}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{t}=\mathrm{2} \\ $$$$\mathrm{z}\left(\mathrm{u}\right)=\mathrm{u}^{\mathrm{2}} \\ $$$$\mathrm{z}\left(\mathrm{u}\right)=\mathrm{u}^{\mathrm{2}} \mathrm{S}\left(\mathrm{u}\right)\Rightarrow \\ $$$$\mathrm{z}'=\mathrm{2us}+\mathrm{u}^{\mathrm{2}} \mathrm{s}' \\ $$$$\mathrm{z}''=\mathrm{4us}'+\mathrm{2s}+\mathrm{u}^{\mathrm{2}} \mathrm{s}'^{'} \\ $$$$\Rightarrow\mathrm{4u}^{\mathrm{2}} \left(\mathrm{u}^{\mathrm{2}} \mathrm{s}''+\mathrm{2s}+\mathrm{4us}'\right)−\mathrm{12u}\left(\mathrm{2us}+\mathrm{u}^{\mathrm{2}} \mathrm{s}'\right)+\mathrm{16u}^{\mathrm{2}} \mathrm{s}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4u}^{\mathrm{4}} \mathrm{s}''+\mathrm{4u}^{\mathrm{3}} \mathrm{s}'=\mathrm{0} \\ $$$$\Rightarrow\mathrm{us}''+\mathrm{s}'=\mathrm{0}\Rightarrow\left(\mathrm{us}'\right)'=\mathrm{0}\Rightarrow\mathrm{us}'=\mathrm{c} \\ $$$$\frac{\mathrm{ds}}{\mathrm{du}}=\frac{\mathrm{c}}{\mathrm{u}}\Rightarrow\mathrm{ds}=\frac{\mathrm{c}}{\mathrm{u}}\mathrm{du}\Rightarrow\mathrm{s}=\mathrm{aln}\left(\mathrm{u}\right)+\mathrm{b} \\ $$$$\Rightarrow\mathrm{z}\left(\mathrm{u}\right)=\mathrm{u}^{\mathrm{2}} \left(\mathrm{aln}\left(\mid\mathrm{u}\mid\right)+\mathrm{b}\right) \\ $$$$\mathrm{particular}\:\mathrm{solution} \\ $$$$\mathrm{4u}^{\mathrm{2}} \mathrm{z}''−\mathrm{12uz}'+\mathrm{16z}=\mathrm{u}^{\mathrm{3}} \\ $$$$\mathrm{z}=\mathrm{au}^{\mathrm{3}} \Rightarrow\mathrm{4u}^{\mathrm{2}} \left(\mathrm{6au}\right)−\mathrm{12u}\left(\mathrm{3au}^{\mathrm{2}} \right)+\mathrm{16au}^{\mathrm{3}} =\mathrm{u}^{\mathrm{3}} \\ $$$$\mathrm{a}=\frac{\mathrm{1}}{\mathrm{4}},\mathrm{z}=\frac{\mathrm{u}^{\mathrm{3}} }{\mathrm{4}}\Rightarrow\mathrm{solution}\:\mathrm{of}\:\mathrm{E} \\ $$$$\mathrm{Z}=\mathrm{u}^{\mathrm{2}} \left(\mathrm{aln}\left(\mid\mathrm{u}\mid\right)+\mathrm{b}\right)+\frac{\mathrm{u}^{\mathrm{3}} }{\mathrm{4}} \\ $$$$\mathrm{Y}\left(\mathrm{x}\right)=\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{aln}\mid\mathrm{2x}+\mathrm{1}\mid+\mathrm{b}\right)+\frac{\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{4}} \\ $$
Commented by key of knowledge last updated on 10/Jan/20
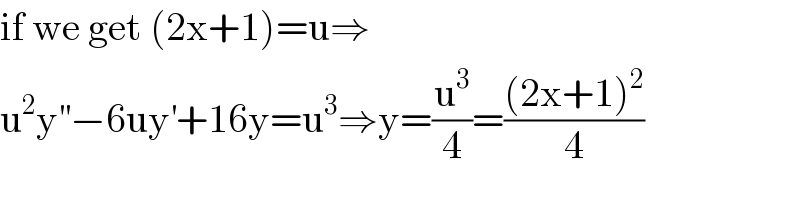
if we get (2x+1)=u⇒ u^2 y^(′′) −6uy^′ +16y=u^3 ⇒y=(u^3 /4)=(((2x+1)^2 )/4)
$$\mathrm{if}\:\mathrm{we}\:\mathrm{get}\:\left(\mathrm{2x}+\mathrm{1}\right)=\mathrm{u}\Rightarrow \\ $$$$\mathrm{u}^{\mathrm{2}} \mathrm{y}^{''} −\mathrm{6uy}^{'} +\mathrm{16y}=\mathrm{u}^{\mathrm{3}} \Rightarrow\mathrm{y}=\frac{\mathrm{u}^{\mathrm{3}} }{\mathrm{4}}=\frac{\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$
Commented by mind is power last updated on 11/Jan/20
forp particular solution yes
$$\mathrm{forp}\:\mathrm{particular}\:\mathrm{solution}\:\:\mathrm{yes} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *