Question Number 8350 by Nayon last updated on 09/Oct/16
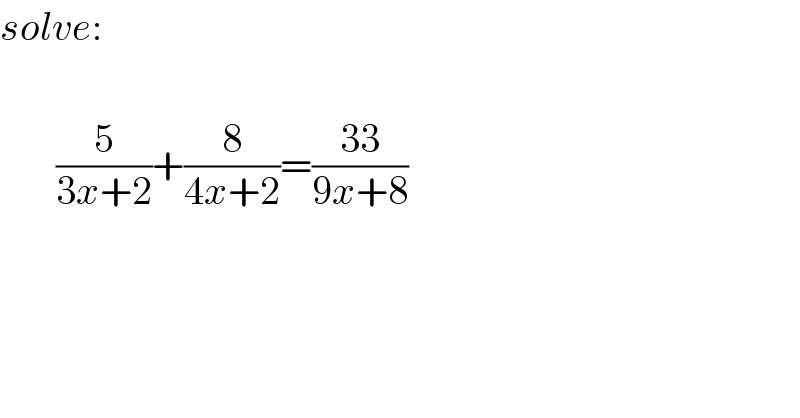
$${solve}: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{5}}{\mathrm{3}{x}+\mathrm{2}}+\frac{\mathrm{8}}{\mathrm{4}{x}+\mathrm{2}}=\frac{\mathrm{33}}{\mathrm{9}{x}+\mathrm{8}} \\ $$
Answered by Rasheed Soomro last updated on 10/Oct/16
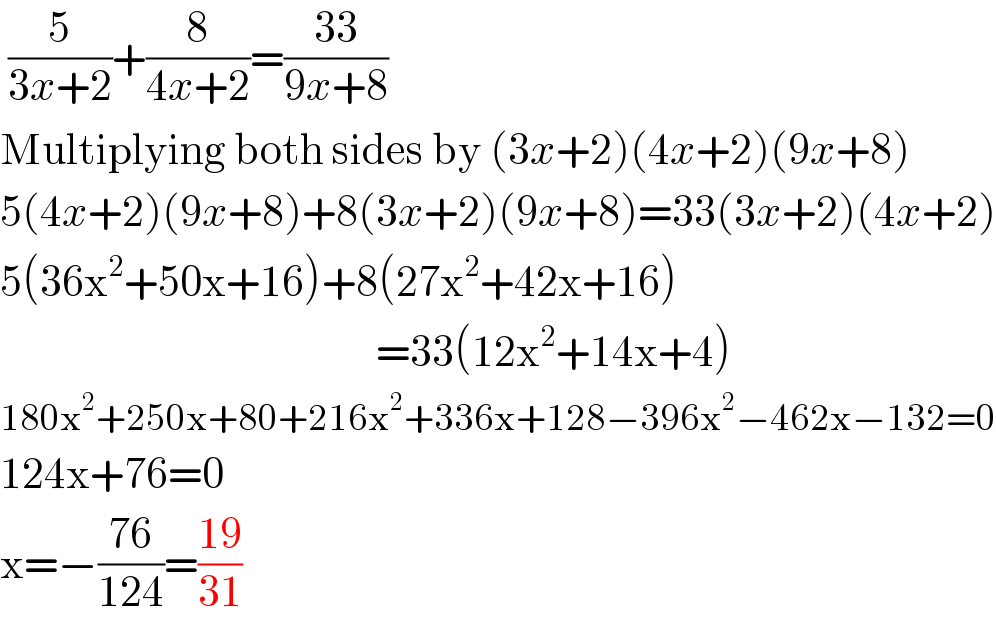
$$\:\frac{\mathrm{5}}{\mathrm{3}{x}+\mathrm{2}}+\frac{\mathrm{8}}{\mathrm{4}{x}+\mathrm{2}}=\frac{\mathrm{33}}{\mathrm{9}{x}+\mathrm{8}} \\ $$$$\mathrm{Multiplying}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{by}\:\left(\mathrm{3}{x}+\mathrm{2}\right)\left(\mathrm{4}{x}+\mathrm{2}\right)\left(\mathrm{9}{x}+\mathrm{8}\right) \\ $$$$\mathrm{5}\left(\mathrm{4}{x}+\mathrm{2}\right)\left(\mathrm{9}{x}+\mathrm{8}\right)+\mathrm{8}\left(\mathrm{3}{x}+\mathrm{2}\right)\left(\mathrm{9}{x}+\mathrm{8}\right)=\mathrm{33}\left(\mathrm{3}{x}+\mathrm{2}\right)\left(\mathrm{4}{x}+\mathrm{2}\right) \\ $$$$\mathrm{5}\left(\mathrm{36x}^{\mathrm{2}} +\mathrm{50x}+\mathrm{16}\right)+\mathrm{8}\left(\mathrm{27x}^{\mathrm{2}} +\mathrm{42x}+\mathrm{16}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{33}\left(\mathrm{12x}^{\mathrm{2}} +\mathrm{14x}+\mathrm{4}\right) \\ $$$$\mathrm{180x}^{\mathrm{2}} +\mathrm{250x}+\mathrm{80}+\mathrm{216x}^{\mathrm{2}} +\mathrm{336x}+\mathrm{128}−\mathrm{396x}^{\mathrm{2}} −\mathrm{462x}−\mathrm{132}=\mathrm{0} \\ $$$$\mathrm{124x}+\mathrm{76}=\mathrm{0} \\ $$$$\mathrm{x}=−\frac{\mathrm{76}}{\mathrm{124}}=\frac{\mathrm{19}}{\mathrm{31}} \\ $$
