Question Number 10836 by okhema last updated on 27/Feb/17
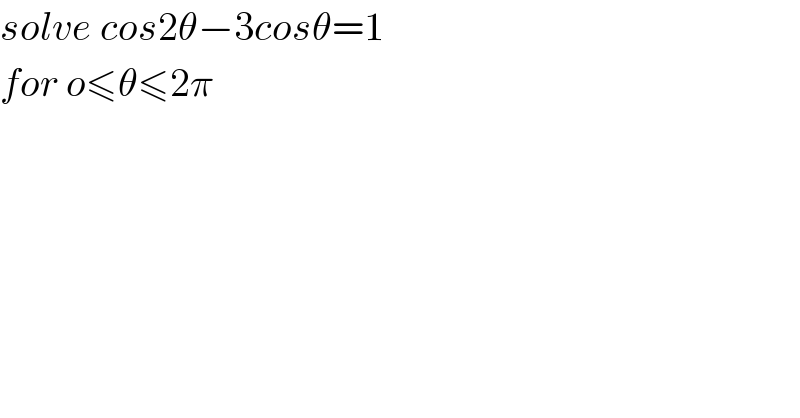
$${solve}\:{cos}\mathrm{2}\theta−\mathrm{3}{cos}\theta=\mathrm{1} \\ $$$${for}\:{o}\leqslant\theta\leqslant\mathrm{2}\pi \\ $$
Answered by ridwan balatif last updated on 27/Feb/17
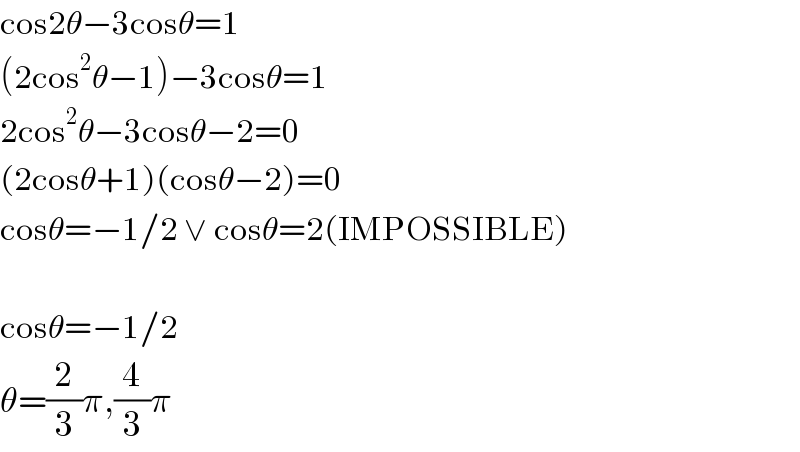
$$\mathrm{cos2}\theta−\mathrm{3cos}\theta=\mathrm{1} \\ $$$$\left(\mathrm{2cos}^{\mathrm{2}} \theta−\mathrm{1}\right)−\mathrm{3cos}\theta=\mathrm{1} \\ $$$$\mathrm{2cos}^{\mathrm{2}} \theta−\mathrm{3cos}\theta−\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{2cos}\theta+\mathrm{1}\right)\left(\mathrm{cos}\theta−\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\theta=−\mathrm{1}/\mathrm{2}\:\vee\:\mathrm{cos}\theta=\mathrm{2}\left(\mathrm{IMPOSSIBLE}\right) \\ $$$$ \\ $$$$\mathrm{cos}\theta=−\mathrm{1}/\mathrm{2} \\ $$$$\theta=\frac{\mathrm{2}}{\mathrm{3}}\pi,\frac{\mathrm{4}}{\mathrm{3}}\pi \\ $$
