Question Number 74367 by Learner-123 last updated on 23/Nov/19
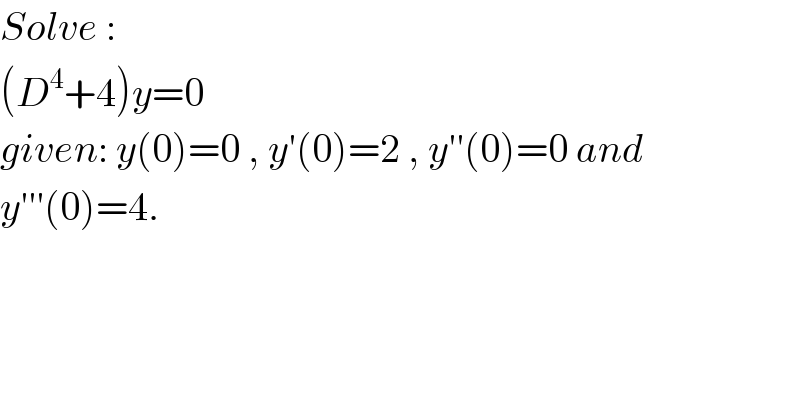
$${Solve}\:: \\ $$$$\left({D}^{\mathrm{4}} +\mathrm{4}\right){y}=\mathrm{0}\: \\ $$$${given}:\:{y}\left(\mathrm{0}\right)=\mathrm{0}\:,\:{y}'\left(\mathrm{0}\right)=\mathrm{2}\:,\:{y}''\left(\mathrm{0}\right)=\mathrm{0}\:{and} \\ $$$${y}'''\left(\mathrm{0}\right)=\mathrm{4}. \\ $$
Commented by mr W last updated on 23/Nov/19

$${please}\:{check}\:{question}\:{and}\:{answer}. \\ $$$${if}\:{question}\:{is}\:{correct},\:{answer}\:{should}\:{be} \\ $$$${y}=\frac{{e}^{\sqrt{\mathrm{2}}{x}} −{e}^{−\sqrt{\mathrm{2}}{x}} }{\:\sqrt{\mathrm{2}}} \\ $$
Commented by Learner-123 last updated on 23/Nov/19
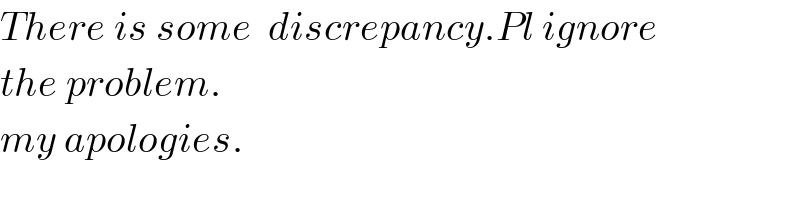
$${There}\:{is}\:{some}\:\:{discrepancy}.{Pl}\:{ignore} \\ $$$${the}\:{problem}. \\ $$$${my}\:{apologies}. \\ $$
