Question Number 132082 by liberty last updated on 11/Feb/21
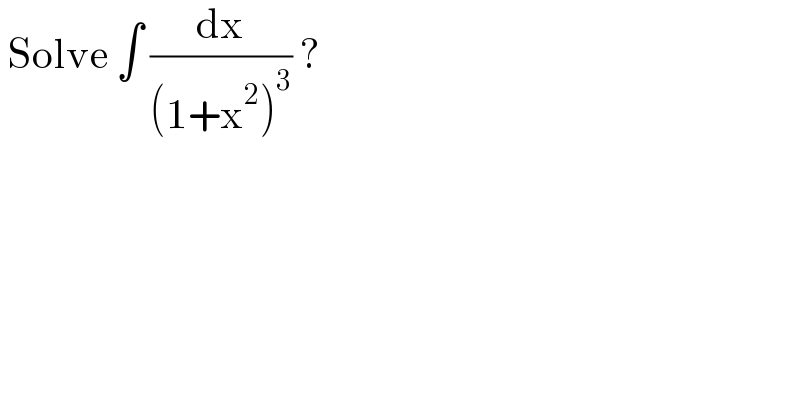
$$\:\mathrm{Solve}\:\int\:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\:?\: \\ $$
Answered by EDWIN88 last updated on 11/Feb/21
![Ostrogradski method Consider (d/dx)(((ax^3 +bx)/((x^2 +1)^2 )) )= ((−ax^4 +(3a−3b)x^2 +b)/((x^2 +1)^3 )) ∫ (d/dx)[((ax^3 +bx)/((x^2 +1)^2 )) ] = ∫ ((−ax^4 +(3a−3b)x^2 +b)/((x^2 +1)^3 )) dx+∫ (c/(x^2 +1))dx comparing coefficients 1= −ax^4 +(3a−3b)x^2 +c(x^2 +1)^2 +b 1= (c−a)x^4 +(3a−3b+2c)x^2 +b+c we get a=c , b+c = 1 , 3a−3b+2c = 0 then a=c=(3/8) ; b=(5/8) therefore I=(1/8)[((3x^3 +5x)/((x^2 +1)^2 )) ]+(3/8)∫ (dx/(x^2 +1)) I= (1/8) [ ((3x^3 +5x)/((x^2 +1)^2 )) ] + (3/8)arctan (x) + c please check](https://www.tinkutara.com/question/Q132083.png)
$$\mathrm{Ostrogradski}\:\mathrm{method} \\ $$$$\mathrm{Consider}\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{ax}^{\mathrm{3}} +\mathrm{bx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\right)=\:\frac{−\mathrm{ax}^{\mathrm{4}} +\left(\mathrm{3a}−\mathrm{3b}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{b}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\int\:\frac{\mathrm{d}}{\mathrm{dx}}\left[\frac{\mathrm{ax}^{\mathrm{3}} +\mathrm{bx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\right]\:=\:\int\:\frac{−\mathrm{ax}^{\mathrm{4}} +\left(\mathrm{3a}−\mathrm{3b}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{b}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:\mathrm{dx}+\int\:\frac{\mathrm{c}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\mathrm{comparing}\:\mathrm{coefficients} \\ $$$$\:\mathrm{1}=\:−\mathrm{ax}^{\mathrm{4}} +\left(\mathrm{3a}−\mathrm{3b}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{c}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +\mathrm{b} \\ $$$$\:\mathrm{1}=\:\left(\mathrm{c}−\mathrm{a}\right)\mathrm{x}^{\mathrm{4}} +\left(\mathrm{3a}−\mathrm{3b}+\mathrm{2c}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{b}+\mathrm{c} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{a}=\mathrm{c}\:,\:\mathrm{b}+\mathrm{c}\:=\:\mathrm{1}\:,\:\mathrm{3a}−\mathrm{3b}+\mathrm{2c}\:=\:\mathrm{0} \\ $$$$\mathrm{then}\:\mathrm{a}=\mathrm{c}=\frac{\mathrm{3}}{\mathrm{8}}\:;\:\mathrm{b}=\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\mathrm{therefore}\:\mathrm{I}=\frac{\mathrm{1}}{\mathrm{8}}\left[\frac{\mathrm{3x}^{\mathrm{3}} +\mathrm{5x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\right]+\frac{\mathrm{3}}{\mathrm{8}}\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{8}}\:\left[\:\frac{\mathrm{3x}^{\mathrm{3}} +\mathrm{5x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\right]\:+\:\frac{\mathrm{3}}{\mathrm{8}}\mathrm{arctan}\:\left(\mathrm{x}\right)\:+\:\mathrm{c} \\ $$$$\mathrm{please}\:\mathrm{check} \\ $$
Answered by liberty last updated on 11/Feb/21

$$\mathrm{by}\:\mathrm{Ostrogradski}\:\mathrm{method} \\ $$$$\mathrm{let}\:\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:=\:\frac{\mathrm{ax}^{\mathrm{3}} +\mathrm{bx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\:\int\:\frac{\mathrm{c}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\mathrm{differentiating}\:\mathrm{both}\:\mathrm{sides} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:=\:\frac{\left(\mathrm{3ax}^{\mathrm{2}} +\mathrm{b}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{ax}^{\mathrm{3}} +\mathrm{bx}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{c}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:=\:\frac{\left(\mathrm{3ax}^{\mathrm{2}} +\mathrm{b}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)−\left(\mathrm{4ax}^{\mathrm{4}} +\mathrm{4bx}^{\mathrm{2}} \right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{c}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\mathrm{1}=\:\mathrm{3ax}^{\mathrm{4}} +\mathrm{3ax}^{\mathrm{2}} +\mathrm{bx}^{\mathrm{2}} +\mathrm{b}−\mathrm{4ax}^{\mathrm{4}} −\mathrm{4bx}^{\mathrm{2}} +\mathrm{cx}^{\mathrm{4}} +\mathrm{2cx}^{\mathrm{2}} +\mathrm{c} \\ $$$$\mathrm{1}=\left(−\mathrm{a}+\mathrm{c}\right)\mathrm{x}^{\mathrm{4}} +\left(\mathrm{3a}−\mathrm{3b}+\mathrm{2c}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{b}+\mathrm{c} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{c}=\mathrm{a}\:;\:\mathrm{b}+\mathrm{c}=\mathrm{1}\:;\:\mathrm{3a}−\mathrm{3b}+\mathrm{2c}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{5c}−\mathrm{3}\left(\mathrm{1}−\mathrm{c}\right)=\mathrm{0}\:;\:\mathrm{8c}=\mathrm{3} \\ $$$$\mathrm{c}=\mathrm{a}=\frac{\mathrm{3}}{\mathrm{8}}\:\mathrm{and}\:\mathrm{b}=\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{become}\: \\ $$$$\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:=\:\frac{\mathrm{3x}^{\mathrm{3}} +\mathrm{5x}}{\mathrm{8}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:+\int\:\frac{\mathrm{3}}{\mathrm{8}}\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3x}^{\mathrm{3}} +\mathrm{5x}}{\mathrm{8}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{3}}{\mathrm{8}}\mathrm{arctan}\:\mathrm{x}\:+\:\mathrm{c} \\ $$$$ \\ $$
