Question Number 5908 by sanusihammed last updated on 04/Jun/16
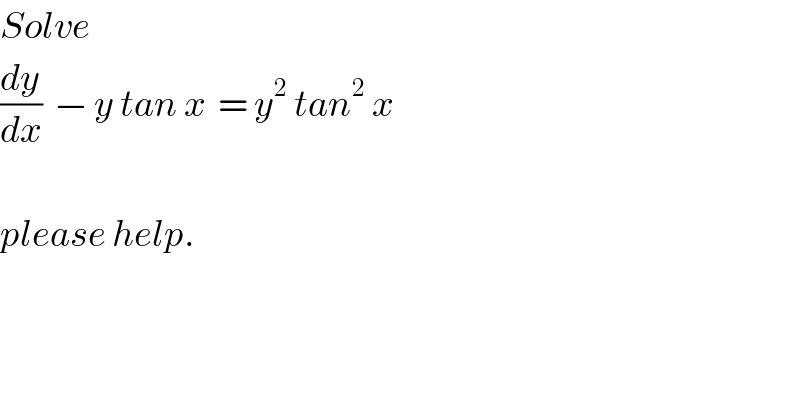
$${Solve}\:\: \\ $$$$\frac{{dy}}{{dx}}\:\:−\:{y}\:{tan}\:{x}\:\:=\:{y}^{\mathrm{2}} \:{tan}^{\mathrm{2}} \:{x} \\ $$$$ \\ $$$${please}\:{help}. \\ $$
Commented by 123456 last updated on 05/Jun/16
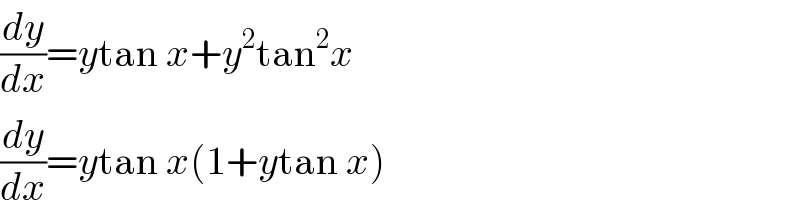
$$\frac{{dy}}{{dx}}={y}\mathrm{tan}\:{x}+{y}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} {x} \\ $$$$\frac{{dy}}{{dx}}={y}\mathrm{tan}\:{x}\left(\mathrm{1}+{y}\mathrm{tan}\:{x}\right) \\ $$
Commented by nburiburu last updated on 25/Jun/16
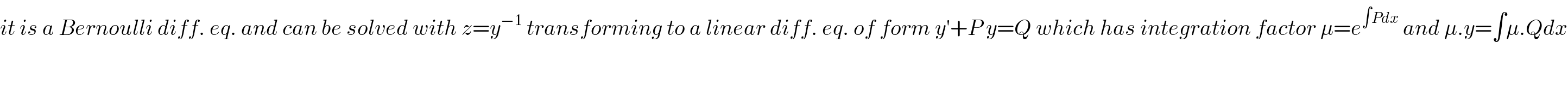
$${it}\:{is}\:{a}\:{Bernoulli}\:{diff}.\:{eq}.\:{and}\:{can}\:{be}\:{solved}\:{with}\:{z}={y}^{−\mathrm{1}} \:{transforming}\:{to}\:{a}\:{linear}\:{diff}.\:{eq}.\:{of}\:{form}\:{y}'+{P}\:{y}={Q}\:{which}\:{has}\:{integration}\:{factor}\:\mu={e}^{\int{Pdx}} \:{and}\:\mu.{y}=\int\mu.{Qdx} \\ $$
