Question Number 1828 by Filup last updated on 07/Oct/15

$$\mathrm{Solve}\:\mathrm{for}\:{a}\:\mathrm{and}\:\mathrm{explain}\:\mathrm{your}\:\mathrm{working} \\ $$$${a}={e}^{{a}} \\ $$
Commented by Alejandro Prieto last updated on 14/Oct/15

$$\mathrm{Gr}\acute {\mathrm{a}ficamente}\:\mathrm{podr}\acute {\mathrm{i}a}\:\mathrm{verse}\:\mathrm{que}\:\mathrm{las}\:\mathrm{funciones} \\ $$$${f}\left({x}\right)\:=\:{e}^{{x}} \:\mathrm{y}\:{g}\left({x}\right)\:=\:{x} \\ $$$$\mathrm{no}\:\mathrm{intersectan}\:\mathrm{en}\:\mathrm{ning}\acute {\mathrm{u}n}\:\mathrm{punto}. \\ $$$$\mathrm{Por}\:\mathrm{tanto},\:\mathrm{puede}\:\mathrm{pensarse}\:\mathrm{que}\:\mathrm{no}\:\mathrm{existen}\:\mathrm{soluciones}\:\mathrm{en}\:\mathbb{R}. \\ $$
Commented by 123456 last updated on 16/Oct/15
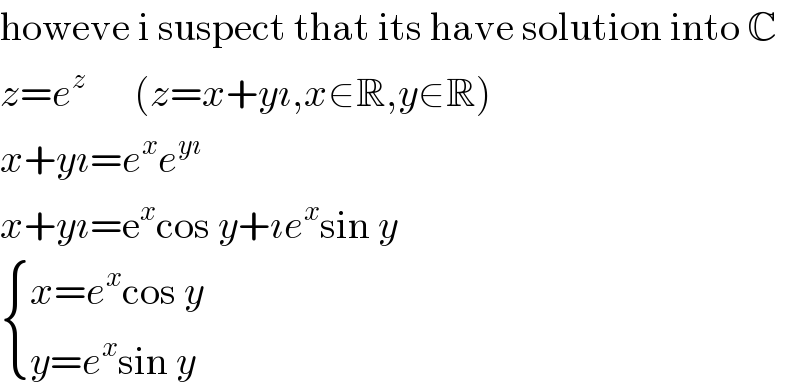
$$\mathrm{howeve}\:\mathrm{i}\:\mathrm{suspect}\:\mathrm{that}\:\mathrm{its}\:\mathrm{have}\:\mathrm{solution}\:\mathrm{into}\:\mathbb{C} \\ $$$${z}={e}^{{z}} \:\:\:\:\:\:\left({z}={x}+{y}\imath,{x}\in\mathbb{R},{y}\in\mathbb{R}\right) \\ $$$${x}+{y}\imath={e}^{{x}} {e}^{{y}\imath} \\ $$$${x}+{y}\imath=\mathrm{e}^{{x}} \mathrm{cos}\:{y}+\imath{e}^{{x}} \mathrm{sin}\:{y} \\ $$$$\begin{cases}{{x}={e}^{{x}} \mathrm{cos}\:{y}}\\{{y}={e}^{{x}} \mathrm{sin}\:{y}}\end{cases} \\ $$
Answered by 123456 last updated on 08/Oct/15
![f(x)=e^x −x f(x)=0⇔e^x −x=0⇔e^x =x x∈R e^x ≥0 x≤0≤e^x so if it as a real solution it would be at [0,+∞) f(0)=e^0 −0=1≠0 f′(x)=e^x −1 x≥0,e^x ≥1⇒f′(x)≥0 so f is increasing into [0,+∞) lets x>0, by mean value theorem into [0,x],∀ξ∈[0,x] with g(x)=e^x g′(ξ)=((e^x −1)/(x−0)) g′(ξ)=e^ξ ≥1,∀ξ≥0 ((e^x −1)/x)≥1 e^x −1≥x e^x −x−1≥0 f(x)−1≥0 f(x)≥1](https://www.tinkutara.com/question/Q1829.png)
$${f}\left({x}\right)={e}^{{x}} −{x} \\ $$$${f}\left({x}\right)=\mathrm{0}\Leftrightarrow{e}^{{x}} −{x}=\mathrm{0}\Leftrightarrow{e}^{{x}} ={x} \\ $$$${x}\in\mathbb{R} \\ $$$${e}^{{x}} \geqslant\mathrm{0} \\ $$$${x}\leqslant\mathrm{0}\leqslant{e}^{{x}} \\ $$$$\mathrm{so}\:\mathrm{if}\:\mathrm{it}\:\mathrm{as}\:\mathrm{a}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{it}\:\mathrm{would}\:\mathrm{be}\:\mathrm{at} \\ $$$$\left[\mathrm{0},+\infty\right) \\ $$$${f}\left(\mathrm{0}\right)={e}^{\mathrm{0}} −\mathrm{0}=\mathrm{1}\neq\mathrm{0} \\ $$$${f}'\left({x}\right)={e}^{{x}} −\mathrm{1} \\ $$$${x}\geqslant\mathrm{0},{e}^{{x}} \geqslant\mathrm{1}\Rightarrow{f}'\left({x}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{so}\:{f}\:\mathrm{is}\:\mathrm{increasing}\:\mathrm{into}\:\left[\mathrm{0},+\infty\right) \\ $$$$\mathrm{lets}\:{x}>\mathrm{0},\:\mathrm{by}\:\mathrm{mean}\:\mathrm{value}\:\mathrm{theorem}\:\mathrm{into} \\ $$$$\left[\mathrm{0},{x}\right],\forall\xi\in\left[\mathrm{0},{x}\right]\:\mathrm{with}\:{g}\left({x}\right)={e}^{{x}} \\ $$$${g}'\left(\xi\right)=\frac{{e}^{{x}} −\mathrm{1}}{{x}−\mathrm{0}} \\ $$$${g}'\left(\xi\right)={e}^{\xi} \geqslant\mathrm{1},\forall\xi\geqslant\mathrm{0} \\ $$$$\frac{{e}^{{x}} −\mathrm{1}}{{x}}\geqslant\mathrm{1} \\ $$$${e}^{{x}} −\mathrm{1}\geqslant{x} \\ $$$${e}^{{x}} −{x}−\mathrm{1}\geqslant\mathrm{0} \\ $$$${f}\left({x}\right)−\mathrm{1}\geqslant\mathrm{0} \\ $$$${f}\left({x}\right)\geqslant\mathrm{1} \\ $$
