Menu Close

Solve-for-ve-integers-gt-0-x-2-y-4-z-6-

Tinku Tara 0 Comments
Pin




Question Number 4230 by prakash jain last updated on 03/Jan/16
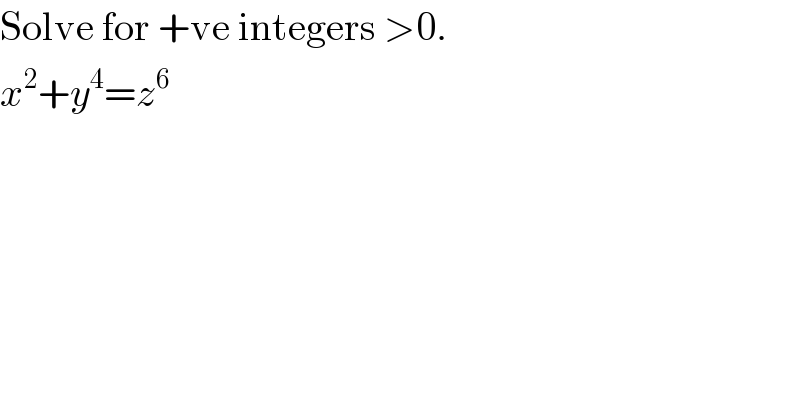
Solve for +ve integers >0. x^2 +y^4 =z^6
$$\mathrm{Solve}\:\mathrm{for}\:+\mathrm{ve}\:\mathrm{integers}\:>\mathrm{0}. \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{4}} ={z}^{\mathrm{6}} \\ $$
Commented by Rasheed Soomro last updated on 04/Jan/16
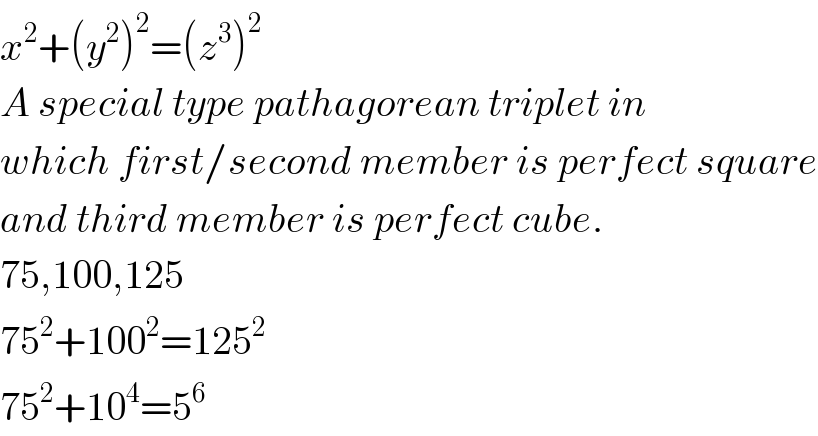
x^2 +(y^2 )^2 =(z^3 )^2 A special type pathagorean triplet in which first/second member is perfect square and third member is perfect cube. 75,100,125 75^2 +100^2 =125^2 75^2 +10^4 =5^6
$${x}^{\mathrm{2}} +\left({y}^{\mathrm{2}} \right)^{\mathrm{2}} =\left({z}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$${A}\:{special}\:{type}\:{pathagorean}\:{triplet}\:{in} \\ $$$${which}\:{first}/{second}\:{member}\:{is}\:{perfect}\:{square} \\ $$$${and}\:{third}\:{member}\:{is}\:{perfect}\:{cube}. \\ $$$$\mathrm{75},\mathrm{100},\mathrm{125} \\ $$$$\mathrm{75}^{\mathrm{2}} +\mathrm{100}^{\mathrm{2}} =\mathrm{125}^{\mathrm{2}} \\ $$$$\mathrm{75}^{\mathrm{2}} +\mathrm{10}^{\mathrm{4}} =\mathrm{5}^{\mathrm{6}} \\ $$
Answered by Rasheed Soomro last updated on 05/Jan/16
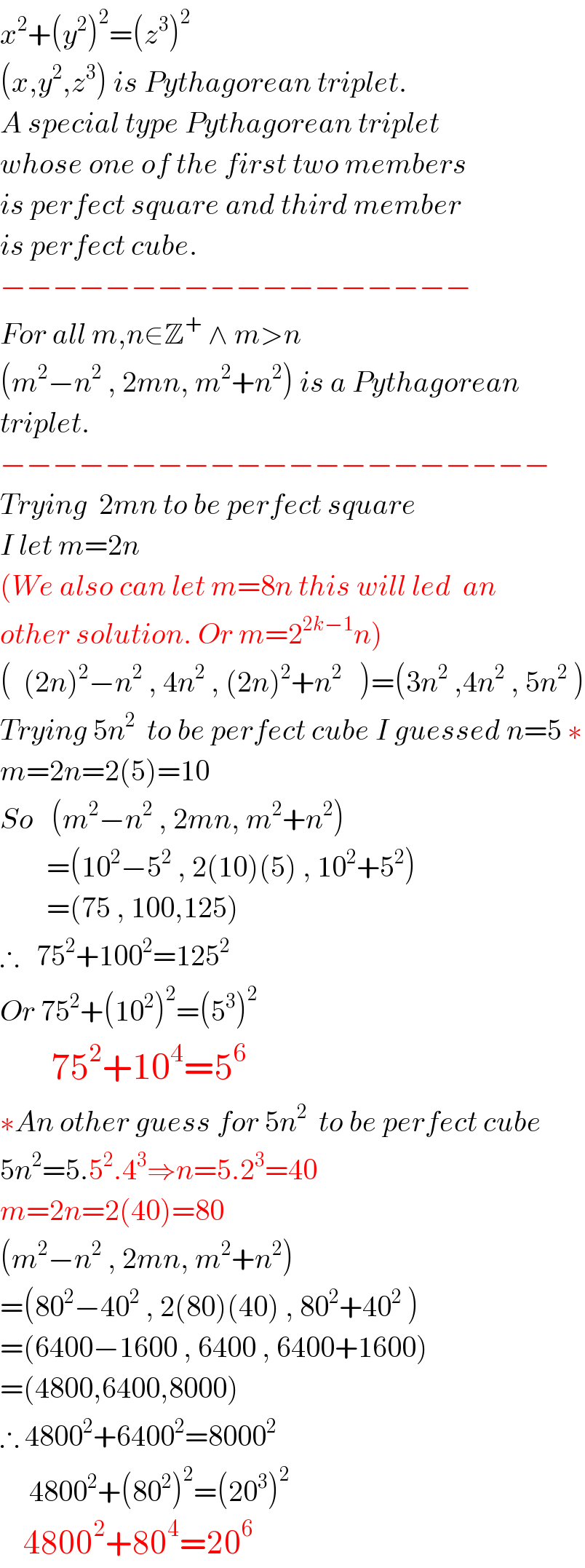
x^2 +(y^2 )^2 =(z^3 )^2 (x,y^2 ,z^3 ) is Pythagorean triplet. A special type Pythagorean triplet whose one of the first two members is perfect square and third member is perfect cube. −−−−−−−−−−−−−−−−−− For all m,n∈Z^+ ∧ m>n (m^2 −n^2 , 2mn, m^2 +n^2 ) is a Pythagorean triplet. −−−−−−−−−−−−−−−−−−−−− Trying 2mn to be perfect square I let m=2n (We also can let m=8n this will led an other solution. Or m=2^(2k−1) n) ( (2n)^2 −n^2 , 4n^2 , (2n)^2 +n^2 )=(3n^2 ,4n^2 , 5n^2 ) Trying 5n^2 to be perfect cube I guessed n=5 ∗ m=2n=2(5)=10 So (m^2 −n^2 , 2mn, m^2 +n^2 ) =(10^2 −5^2 , 2(10)(5) , 10^2 +5^2 ) =(75 , 100,125) ∴ 75^2 +100^2 =125^2 Or 75^2 +(10^2 )^2 =(5^3 )^2 75^2 +10^4 =5^6 ∗An other guess for 5n^2 to be perfect cube 5n^2 =5.5^2 .4^3 ⇒n=5.2^3 =40 m=2n=2(40)=80 (m^2 −n^2 , 2mn, m^2 +n^2 ) =(80^2 −40^2 , 2(80)(40) , 80^2 +40^2 ) =(6400−1600 , 6400 , 6400+1600) =(4800,6400,8000) ∴ 4800^2 +6400^2 =8000^2 4800^2 +(80^2 )^2 =(20^3 )^2 4800^2 +80^4 =20^6
$${x}^{\mathrm{2}} +\left({y}^{\mathrm{2}} \right)^{\mathrm{2}} =\left({z}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\left({x},{y}^{\mathrm{2}} ,{z}^{\mathrm{3}} \right)\:{is}\:{Pythagorean}\:{triplet}. \\ $$$${A}\:{special}\:{type}\:{Pythagorean}\:{triplet} \\ $$$${whose}\:{one}\:{of}\:{the}\:{first}\:{two}\:{members} \\ $$$${is}\:{perfect}\:{square}\:{and}\:{third}\:{member} \\ $$$${is}\:{perfect}\:{cube}. \\ $$$$−−−−−−−−−−−−−−−−−− \\ $$$${For}\:{all}\:{m},{n}\in\mathbb{Z}^{+} \:\wedge\:{m}>{n} \\ $$$$\left({m}^{\mathrm{2}} −{n}^{\mathrm{2}} \:,\:\mathrm{2}{mn},\:{m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)\:{is}\:{a}\:{Pythagorean} \\ $$$${triplet}. \\ $$$$−−−−−−−−−−−−−−−−−−−−− \\ $$$${Trying}\:\:\mathrm{2}{mn}\:{to}\:{be}\:{perfect}\:{square} \\ $$$${I}\:{let}\:{m}=\mathrm{2}{n} \\ $$$$\left({We}\:{also}\:{can}\:{let}\:{m}=\mathrm{8}{n}\:{this}\:{will}\:{led}\:\:{an}\right. \\ $$$$\left.{other}\:{solution}.\:{Or}\:{m}=\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} {n}\right) \\ $$$$\left(\:\:\left(\mathrm{2}{n}\right)^{\mathrm{2}} −{n}^{\mathrm{2}} \:,\:\mathrm{4}{n}^{\mathrm{2}} \:,\:\left(\mathrm{2}{n}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} \:\:\:\right)=\left(\mathrm{3}{n}^{\mathrm{2}} \:,\mathrm{4}{n}^{\mathrm{2}} \:,\:\mathrm{5}{n}^{\mathrm{2}} \:\right) \\ $$$${Trying}\:\mathrm{5}{n}^{\mathrm{2}} \:\:{to}\:{be}\:{perfect}\:{cube}\:{I}\:{guessed}\:{n}=\mathrm{5}\:\ast \\ $$$${m}=\mathrm{2}{n}=\mathrm{2}\left(\mathrm{5}\right)=\mathrm{10} \\ $$$${So}\:\:\:\left({m}^{\mathrm{2}} −{n}^{\mathrm{2}} \:,\:\mathrm{2}{mn},\:{m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:=\left(\mathrm{10}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} \:,\:\mathrm{2}\left(\mathrm{10}\right)\left(\mathrm{5}\right)\:,\:\mathrm{10}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:=\left(\mathrm{75}\:,\:\mathrm{100},\mathrm{125}\right) \\ $$$$\therefore\:\:\:\mathrm{75}^{\mathrm{2}} +\mathrm{100}^{\mathrm{2}} =\mathrm{125}^{\mathrm{2}} \\ $$$${Or}\:\mathrm{75}^{\mathrm{2}} +\left(\mathrm{10}^{\mathrm{2}} \right)^{\mathrm{2}} =\left(\mathrm{5}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\mathrm{75}^{\mathrm{2}} +\mathrm{10}^{\mathrm{4}} =\mathrm{5}^{\mathrm{6}} \\ $$$$\ast{An}\:{other}\:{guess}\:{for}\:\mathrm{5}{n}^{\mathrm{2}} \:\:{to}\:{be}\:{perfect}\:{cube} \\ $$$$\mathrm{5}{n}^{\mathrm{2}} =\mathrm{5}.\mathrm{5}^{\mathrm{2}} .\mathrm{4}^{\mathrm{3}} \Rightarrow{n}=\mathrm{5}.\mathrm{2}^{\mathrm{3}} =\mathrm{40} \\ $$$${m}=\mathrm{2}{n}=\mathrm{2}\left(\mathrm{40}\right)=\mathrm{80} \\ $$$$\left({m}^{\mathrm{2}} −{n}^{\mathrm{2}} \:,\:\mathrm{2}{mn},\:{m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right) \\ $$$$=\left(\mathrm{80}^{\mathrm{2}} −\mathrm{40}^{\mathrm{2}} \:,\:\mathrm{2}\left(\mathrm{80}\right)\left(\mathrm{40}\right)\:,\:\mathrm{80}^{\mathrm{2}} +\mathrm{40}^{\mathrm{2}} \:\right) \\ $$$$=\left(\mathrm{6400}−\mathrm{1600}\:,\:\mathrm{6400}\:,\:\mathrm{6400}+\mathrm{1600}\right) \\ $$$$=\left(\mathrm{4800},\mathrm{6400},\mathrm{8000}\right) \\ $$$$\therefore\:\mathrm{4800}^{\mathrm{2}} +\mathrm{6400}^{\mathrm{2}} =\mathrm{8000}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{4800}^{\mathrm{2}} +\left(\mathrm{80}^{\mathrm{2}} \right)^{\mathrm{2}} =\left(\mathrm{20}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{4800}^{\mathrm{2}} +\mathrm{80}^{\mathrm{4}} =\mathrm{20}^{\mathrm{6}} \\ $$
Answered by Rasheed Soomro last updated on 05/Jan/16
General Solution x^2 +(y)^2 =(z^3 )^2 (x,y^2 ,z^3 ) is Pythagorean triplet. −−−−−−−−−−−−−−−− For m>n and m,n∈N one general Pythagorean triplet is (m^2 −n^2 ,2mn,m^2 +n^2 ) −−−−−−−−−−−−−−−−− To make 2mn perfect square Let m=2^(2k−1) n 2mn=2(2^(2k−1) n)n=2^(2k) n^2 m^2 +n^2 =(2^(2k−1) n)^2 +n^2 =(2^(4k−2) +1)n^2 In order to make m^2 +n^2 perfect cube Let n=2^(4k−2) +1 ∴ m=2^(2k−1) n=2^(2k−1) ×(2^(4k−2) +1)=2^(6k−3) +2^(2k−1) −−−−−−− m^2 −n^2 =(2^(6k−3) +2^(2k−1) )^2 −(2^(4k−2) +1)^2 =2^(12k−6) +2^(4k−2) +2^(8k−3) −2^(8k−4) −1−2^(4k−1) 2mn=2^(2k) (2^(4k−2) +1)^2 ={2^k (2^(4k−2) +1)}^2 m^2 +n^2 =(2^(4k−2) +1)^3 {(2^(6k−3) +2^(2k−1) )^2 −(2^(4k−2) +1)^2 }^2 +{ 2^k (2^(4k−2) +1)}^4 =(2^(4k−2) +1)^6 ∀ k∈N (x,y,z)=((2^(6k−3) +2^(2k−1) )^2 −(2^(4k−2) +1)^2 , 2^k (2^(4k−2) +1),2^(4k−2) +1) For k=1 75^2 +10^4 =5^6
$$\mathrm{General}\:\mathrm{Solution} \\ $$$${x}^{\mathrm{2}} +\left({y}\right)^{\mathrm{2}} =\left({z}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\left({x},{y}^{\mathrm{2}} ,{z}^{\mathrm{3}} \right)\:{is}\:{Pythagorean}\:{triplet}. \\ $$$$−−−−−−−−−−−−−−−− \\ $$$${For}\:{m}>{n}\:{and}\:{m},{n}\in\mathbb{N}\:{one}\:{general} \\ $$$${Pythagorean}\:{triplet}\:{is} \\ $$$$\left({m}^{\mathrm{2}} −{n}^{\mathrm{2}} ,\mathrm{2}{mn},{m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right) \\ $$$$−−−−−−−−−−−−−−−−− \\ $$$${To}\:{make}\:\mathrm{2}{mn}\:{perfect}\:{square} \\ $$$${Let}\:{m}=\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} {n} \\ $$$$\mathrm{2}{mn}=\mathrm{2}\left(\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} {n}\right){n}=\mathrm{2}^{\mathrm{2}{k}} {n}^{\mathrm{2}} \\ $$$${m}^{\mathrm{2}} +{n}^{\mathrm{2}} =\left(\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} {n}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} =\left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right){n}^{\mathrm{2}} \\ $$$${In}\:{order}\:{to}\:{make}\:{m}^{\mathrm{2}} +{n}^{\mathrm{2}} \:{perfect}\:{cube} \\ $$$${Let}\:{n}=\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1} \\ $$$$\therefore\:{m}=\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} {n}=\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} ×\left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right)=\mathrm{2}^{\mathrm{6}{k}−\mathrm{3}} +\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} \\ $$$$−−−−−−− \\ $$$${m}^{\mathrm{2}} −{n}^{\mathrm{2}} =\left(\mathrm{2}^{\mathrm{6}{k}−\mathrm{3}} +\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} \right)^{\mathrm{2}} −\left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\mathrm{2}^{\mathrm{12}{k}−\mathrm{6}} +\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{2}^{\mathrm{8}{k}−\mathrm{3}} −\mathrm{2}^{\mathrm{8}{k}−\mathrm{4}} −\mathrm{1}−\mathrm{2}^{\mathrm{4}{k}−\mathrm{1}} \\ $$$$\mathrm{2}{mn}=\mathrm{2}^{\mathrm{2}{k}} \left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} =\left\{\mathrm{2}^{{k}} \left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right)\right\}^{\mathrm{2}} \\ $$$${m}^{\mathrm{2}} +{n}^{\mathrm{2}} =\left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\left\{\left(\mathrm{2}^{\mathrm{6}{k}−\mathrm{3}} +\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} \right)^{\mathrm{2}} −\left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} +\left\{\:\mathrm{2}^{{k}} \left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right)\right\}^{\mathrm{4}} \:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right)^{\mathrm{6}} \:\:\:\forall\:{k}\in\mathbb{N} \\ $$$$\left({x},{y},{z}\right)=\left(\left(\mathrm{2}^{\mathrm{6}{k}−\mathrm{3}} +\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} \right)^{\mathrm{2}} −\left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \:,\:\mathrm{2}^{{k}} \left(\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right),\mathrm{2}^{\mathrm{4}{k}−\mathrm{2}} +\mathrm{1}\right) \\ $$$${For}\:{k}=\mathrm{1}\:\:\mathrm{75}^{\mathrm{2}} +\mathrm{10}^{\mathrm{4}} =\mathrm{5}^{\mathrm{6}} \\ $$$$ \\ $$
Commented by prakash jain last updated on 05/Jan/16
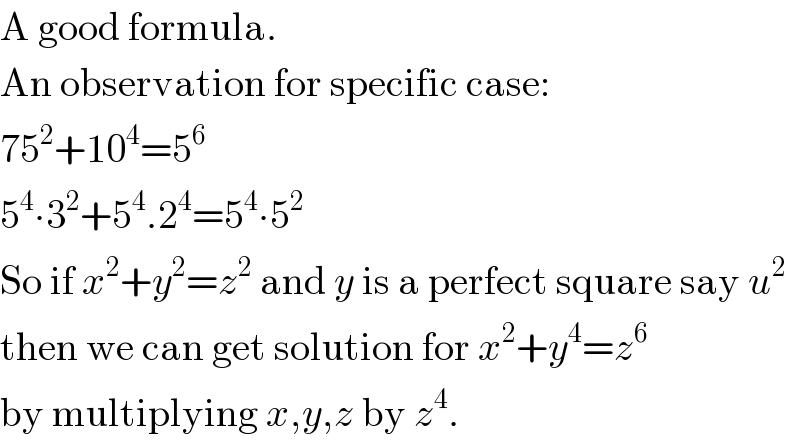
A good formula. An observation for specific case: 75^2 +10^4 =5^6 5^4 ∙3^2 +5^4 .2^4 =5^4 ∙5^2 So if x^2 +y^2 =z^2 and y is a perfect square say u^2 then we can get solution for x^2 +y^4 =z^6 by multiplying x,y,z by z^4 .
$$\mathrm{A}\:\mathrm{good}\:\mathrm{formula}. \\ $$$$\mathrm{An}\:\mathrm{observation}\:\mathrm{for}\:\mathrm{specific}\:\mathrm{case}: \\ $$$$\mathrm{75}^{\mathrm{2}} +\mathrm{10}^{\mathrm{4}} =\mathrm{5}^{\mathrm{6}} \\ $$$$\mathrm{5}^{\mathrm{4}} \centerdot\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{4}} .\mathrm{2}^{\mathrm{4}} =\mathrm{5}^{\mathrm{4}} \centerdot\mathrm{5}^{\mathrm{2}} \\ $$$$\mathrm{So}\:\mathrm{if}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={z}^{\mathrm{2}} \:\mathrm{and}\:{y}\:\mathrm{is}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{square}\:\mathrm{say}\:{u}^{\mathrm{2}} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{can}\:\mathrm{get}\:\mathrm{solution}\:\mathrm{for}\:{x}^{\mathrm{2}} +{y}^{\mathrm{4}} ={z}^{\mathrm{6}} \\ $$$$\mathrm{by}\:\mathrm{multiplying}\:{x},{y},{z}\:\mathrm{by}\:{z}^{\mathrm{4}} . \\ $$
Commented by Rasheed Soomro last updated on 06/Jan/16
G^(OO) D Technique! T HαnkS!
$$\boldsymbol{\mathrm{G}}^{\mathcal{OO}} \boldsymbol{\mathrm{D}}\:\boldsymbol{\mathrm{T}}\mathrm{echnique}!\:\:\mathcal{T}\:\mathcal{H}\alpha{n}\Bbbk\mathcal{S}! \\ $$
Commented by Rasheed Soomro last updated on 08/Jan/16
Pythagorean Triple ▽ Triple satisfying x^2 +y^4 =z^6 Your technique applying twice x^2 +y^2 =z^2 x^2 y^2 +y^2 y^2 =z^2 y^2 (xy)^2 +y^4 =(zy)^2 (xy)^2 (zy)^4 +y^4 (zy)^4 =(zy)^2 (zy)^4 (xy^3 z^2 )^2 +(y^2 z)^4 =(zy)^6 (x,y,z) is Pythagorean triplet ⇒(xy^3 z^2 , y^2 z , zy) is tripletfor x^2 +y^4 =z^6 . (3,4,5)⇒( 3(4)^3 (5)^2 , (4)^2 (5),(5)(4) ) =( 3(64)(25),16(5),20 )=(4800,80,20) (4,3,5)⇒( 4(3)^3 (5)^2 ,(3)^2 (5),(3)(5) )=(2700,45,15)
$${Pythagorean}\:{Triple} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\bigtriangledown \\ $$$$\:{Triple}\:{satisfying}\:{x}^{\mathrm{2}} +{y}^{\mathrm{4}} ={z}^{\mathrm{6}} \\ $$$$\mathrm{Your}\:\mathrm{technique}\:\mathrm{applying}\:\:\mathrm{twice} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={z}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {y}^{\mathrm{2}} ={z}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\left({xy}\right)^{\mathrm{2}} +{y}^{\mathrm{4}} =\left({zy}\right)^{\mathrm{2}} \\ $$$$\left({xy}\right)^{\mathrm{2}} \left({zy}\right)^{\mathrm{4}} +{y}^{\mathrm{4}} \left({zy}\right)^{\mathrm{4}} =\left({zy}\right)^{\mathrm{2}} \left({zy}\right)^{\mathrm{4}} \\ $$$$\left({xy}^{\mathrm{3}} {z}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}^{\mathrm{2}} {z}\right)^{\mathrm{4}} =\left({zy}\right)^{\mathrm{6}} \\ $$$$\left({x},{y},{z}\right)\:{is}\:{Pythagorean}\:{triplet} \\ $$$$\:\:\:\:\:\:\Rightarrow\left({xy}^{\mathrm{3}} {z}^{\mathrm{2}} \:,\:{y}^{\mathrm{2}} {z}\:,\:{zy}\right)\:{is}\:{tripletfor}\:{x}^{\mathrm{2}} +{y}^{\mathrm{4}} ={z}^{\mathrm{6}} . \\ $$$$\left(\mathrm{3},\mathrm{4},\mathrm{5}\right)\Rightarrow\left(\:\mathrm{3}\left(\mathrm{4}\right)^{\mathrm{3}} \left(\mathrm{5}\right)^{\mathrm{2}} ,\:\left(\mathrm{4}\right)^{\mathrm{2}} \left(\mathrm{5}\right),\left(\mathrm{5}\right)\left(\mathrm{4}\right)\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\:\:\mathrm{3}\left(\mathrm{64}\right)\left(\mathrm{25}\right),\mathrm{16}\left(\mathrm{5}\right),\mathrm{20}\:\:\right)=\left(\mathrm{4800},\mathrm{80},\mathrm{20}\right) \\ $$$$\:\left(\mathrm{4},\mathrm{3},\mathrm{5}\right)\Rightarrow\left(\:\mathrm{4}\left(\mathrm{3}\right)^{\mathrm{3}} \left(\mathrm{5}\right)^{\mathrm{2}} ,\left(\mathrm{3}\right)^{\mathrm{2}} \left(\mathrm{5}\right),\left(\mathrm{3}\right)\left(\mathrm{5}\right)\:\right)=\left(\mathrm{2700},\mathrm{45},\mathrm{15}\right) \\ $$
Commented by Rasheed Soomro last updated on 07/Jan/16
(x,y,z) is Pythagorean triplet ⇒(xy^3 z^2 , y^2 z , zy) is required triplet. Let x,y,z are m^2 −n^2 ,2mn , m^2 +n^2 type. xy^3 z^2 =(m^2 −n^2 )(2mn)^3 (m^2 +n^2 )^2 y^2 z=(2mn)^2 (m^2 +n^2 ) yz=(2mn)(m^2 +n^2 ) General Triplet for x^2 +y^4 =z^6 : ((((m^2 −n^2 )(2mn)^3 (m^2 +n^2 )^2 ,)/)(((2mn)^2 (m^2 +n^2 ),)/)(((2mn)(m^2 +n^2 ))/)) Or ((((m^2 −n^2 )^3 (2mn)(m^2 +n^2 )^2 ,)/)(((m^2 −n^2 )^2 (m^2 +n^2 ),)/)(((m^2 −n^2 )(m^2 +n^2 ))/)) ∀ m,n∈N with m>n
$$\left({x},{y},{z}\right)\:{is}\:{Pythagorean}\:{triplet} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\left({xy}^{\mathrm{3}} {z}^{\mathrm{2}} \:,\:{y}^{\mathrm{2}} {z}\:,\:{zy}\right)\:{is}\:{required}\:{triplet}. \\ $$$$\mathrm{Let}\:\:\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{are}\:\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} ,\mathrm{2mn}\:,\:\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \:\mathrm{type}. \\ $$$$\mathrm{xy}^{\mathrm{3}} \mathrm{z}^{\mathrm{2}} =\left(\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} \right)\left(\mathrm{2mn}\right)^{\mathrm{3}} \left(\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{y}^{\mathrm{2}} \mathrm{z}=\left(\mathrm{2mn}\right)^{\mathrm{2}} \left(\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right) \\ $$$$\mathrm{yz}=\left(\mathrm{2mn}\right)\left(\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right) \\ $$$$\mathrm{General}\:\mathrm{Triplet}\:\mathrm{for}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{4}} =\mathrm{z}^{\mathrm{6}} : \\ $$$$\left(\frac{\left(\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} \right)\left(\mathrm{2mn}\right)^{\mathrm{3}} \left(\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right)^{\mathrm{2}} ,}{}\frac{\left(\mathrm{2mn}\right)^{\mathrm{2}} \left(\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right),}{}\frac{\left(\mathrm{2mn}\right)\left(\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right)}{}\right) \\ $$$$\mathrm{Or} \\ $$$$\left(\frac{\left(\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} \right)^{\mathrm{3}} \left(\mathrm{2mn}\right)\left(\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right)^{\mathrm{2}} ,}{}\frac{\left(\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right),}{}\frac{\left(\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} \right)\left(\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right)}{}\right) \\ $$$$\forall\:{m},{n}\in\mathbb{N}\:\:{with}\:{m}>{n} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *