Question Number 77885 by behi83417@gmail.com last updated on 11/Jan/20
![solve for : x 1.(√((x−a)(x−b)))+(√((x−b)(x−c)))+(√((x−c)(x−a)))=d [a,b,c,d∈R try for: a=4,b=3,c=2,d=1] 2. (x−a^2 )(√(x−a))+(x−a)(√(x−a^2 ))=a^2 +a+1 3. (x−a^2 )(√(x^2 −a))+(x^2 −a)(√(x−a^2 ))=a^2 +a+1 [a∈R try for: a=(1/2) ]](https://www.tinkutara.com/question/Q77885.png)
Answered by jagoll last updated on 12/Jan/20
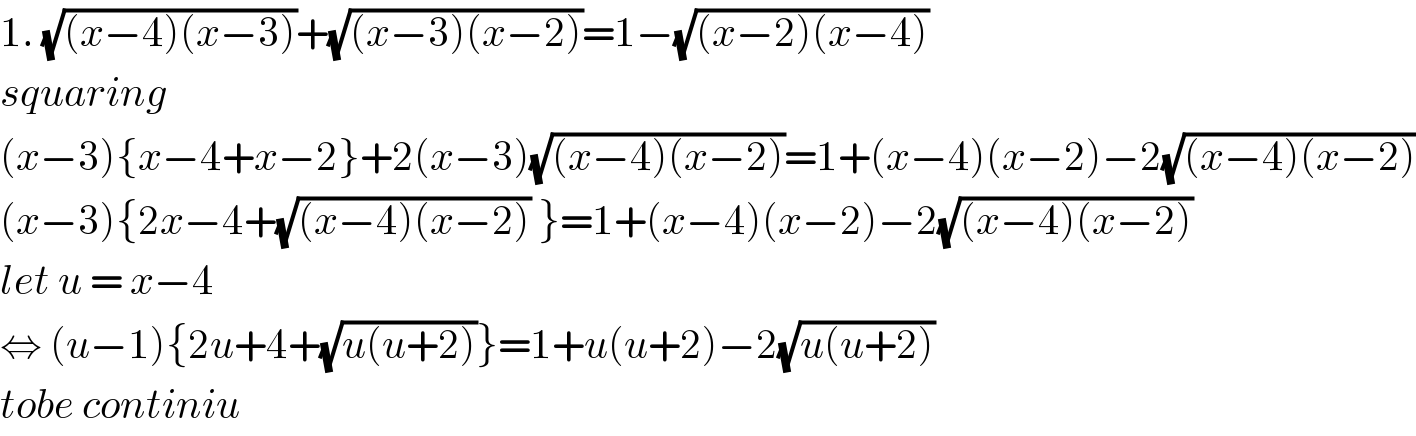
Commented by mr W last updated on 12/Jan/20
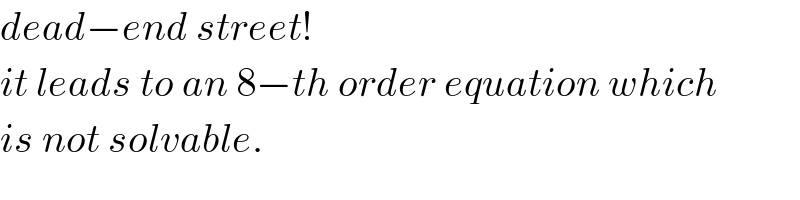
Commented by jagoll last updated on 12/Jan/20
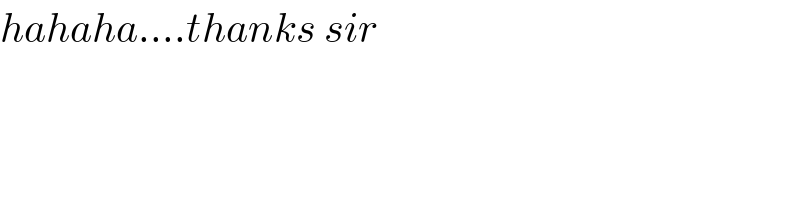
Commented by behi83417@gmail.com last updated on 12/Jan/20

Commented by mr W last updated on 12/Jan/20

Commented by mr W last updated on 12/Jan/20

Commented by mr W last updated on 12/Jan/20
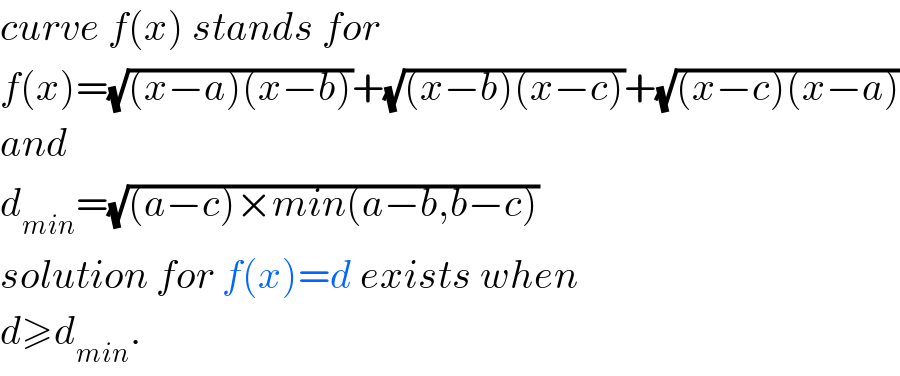
Commented by mr W last updated on 12/Jan/20

Commented by mr W last updated on 12/Jan/20
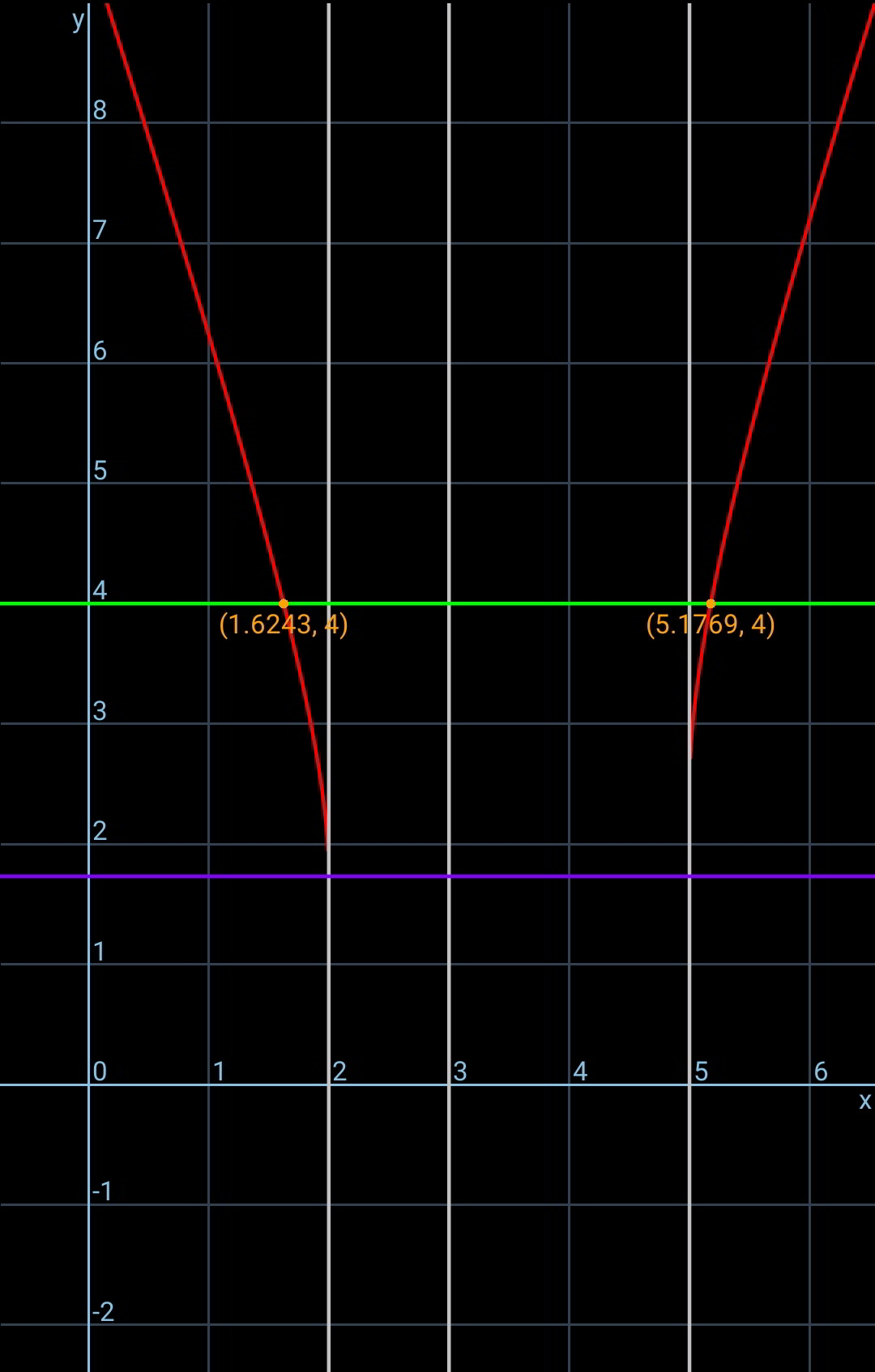
Commented by mr W last updated on 12/Jan/20
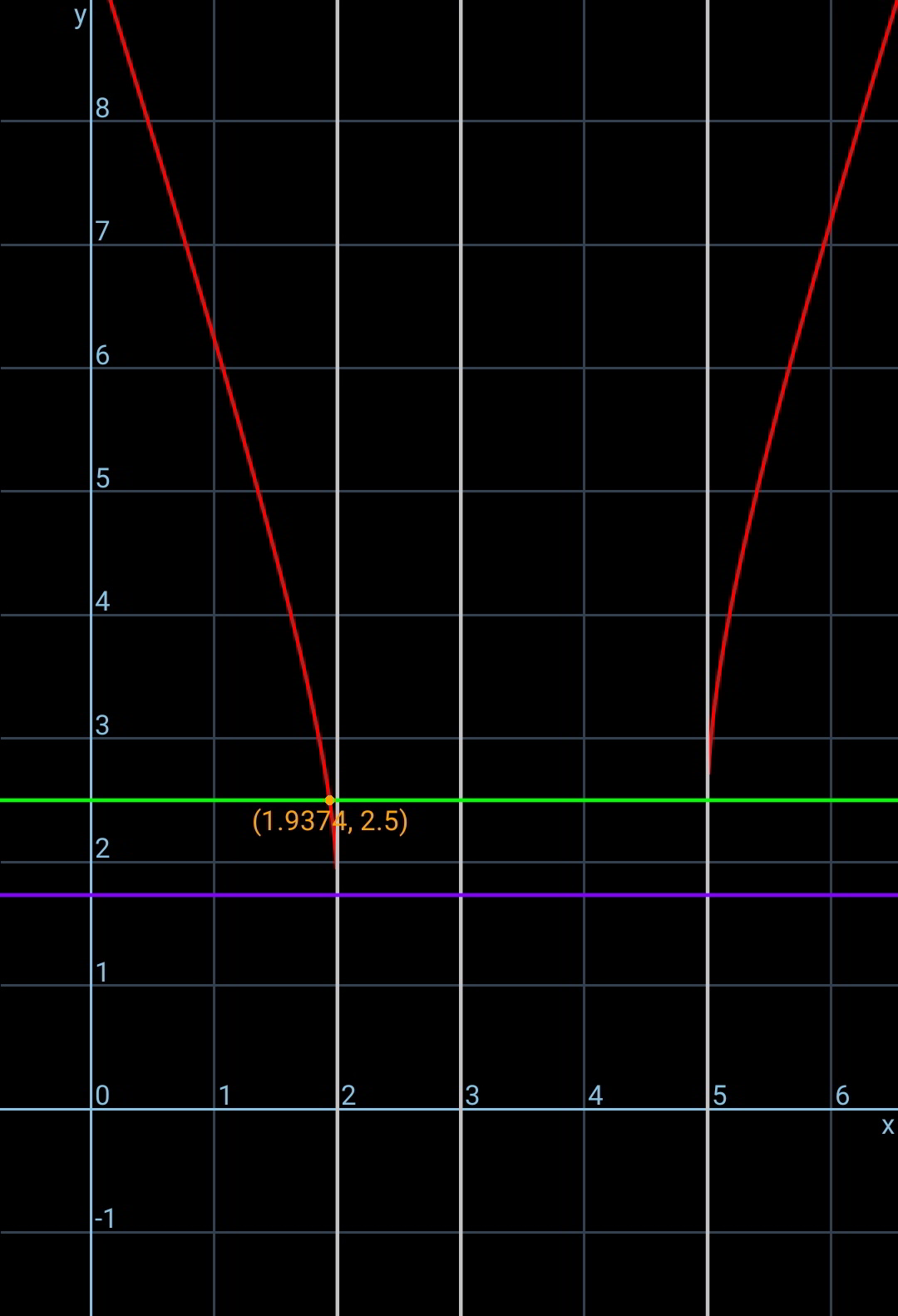
Commented by behi83417@gmail.com last updated on 12/Jan/20

Answered by MJS last updated on 12/Jan/20
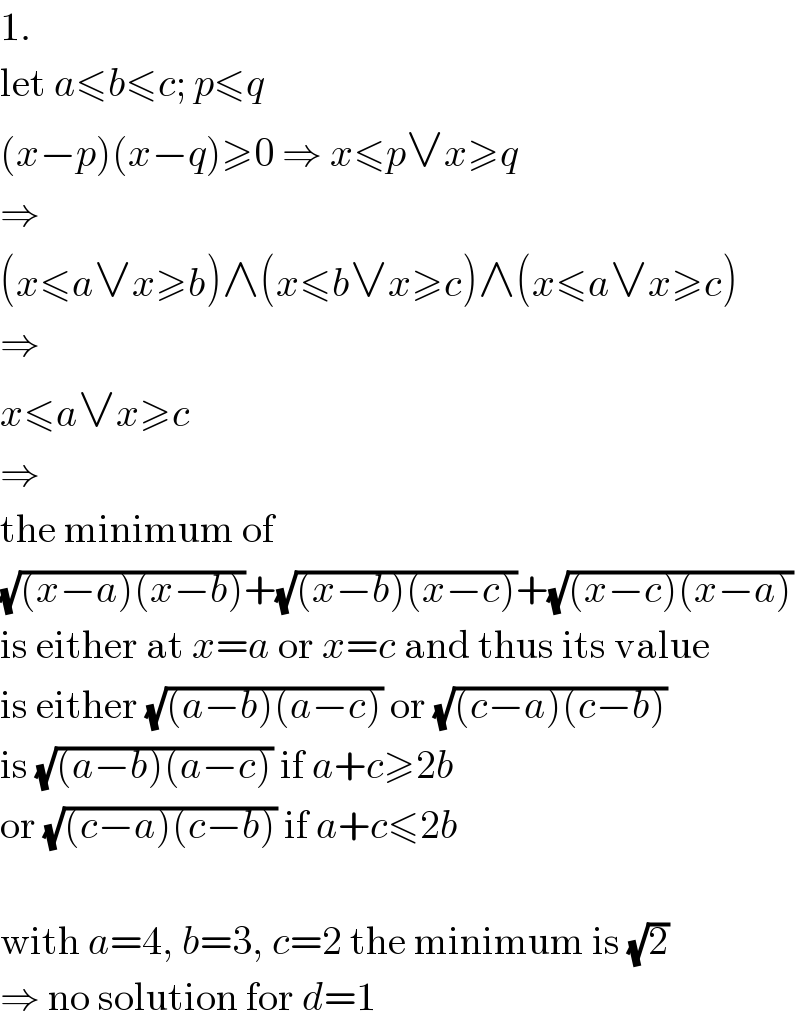
Commented by behi83417@gmail.com last updated on 12/Jan/20

