Question Number 10607 by Saham last updated on 19/Feb/17
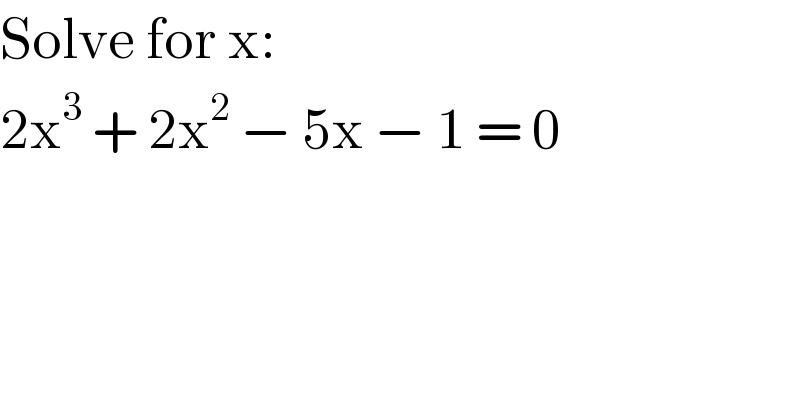
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}: \\ $$$$\mathrm{2x}^{\mathrm{3}} \:+\:\mathrm{2x}^{\mathrm{2}} \:−\:\mathrm{5x}\:−\:\mathrm{1}\:=\:\mathrm{0} \\ $$
Answered by mrW1 last updated on 20/Feb/17

$${a}=\mathrm{2} \\ $$$${b}=\mathrm{2} \\ $$$${c}=−\mathrm{5} \\ $$$${d}=−\mathrm{1} \\ $$$$\Delta={b}^{\mathrm{2}} −\mathrm{3}{ac}=\mathrm{2}^{\mathrm{2}} −\mathrm{3}×\mathrm{2}×\left(−\mathrm{5}\right)=\mathrm{34}>\mathrm{0} \\ $$$${k}=\frac{\mathrm{9}{abc}−\mathrm{2}{b}^{\mathrm{3}} −\mathrm{27}{a}^{\mathrm{2}} {d}}{\mathrm{2}\sqrt{\mid\Delta\mid^{\mathrm{3}} }}=\frac{\mathrm{9}×\mathrm{2}×\mathrm{2}×\left(−\mathrm{5}\right)−\mathrm{2}×\mathrm{2}^{\mathrm{3}} −\mathrm{27}×\mathrm{2}^{\mathrm{2}} ×\left(−\mathrm{1}\right)}{\mathrm{2}×\sqrt{\mathrm{34}^{\mathrm{3}} }}=\frac{−\mathrm{180}−\mathrm{16}+\mathrm{108}}{\mathrm{2}×\mathrm{34}×\sqrt{\mathrm{34}}}=−\frac{\mathrm{22}}{\mathrm{17}×\sqrt{\mathrm{34}}} \\ $$$$\mid{k}\mid<\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}\:{roots} \\ $$$$ \\ $$$$\sqrt{\Delta}=\sqrt{\mathrm{34}} \\ $$$$\frac{\mathrm{cos}^{−\mathrm{1}} {k}}{\mathrm{3}}=\frac{\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{22}}{\mathrm{17}\sqrt{\mathrm{34}}}\right)}{\mathrm{3}}=\mathrm{0}.\mathrm{5982} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{2}\sqrt{\Delta}\mathrm{cos}\:\left(\frac{\mathrm{cos}^{−\mathrm{1}} {k}}{\mathrm{3}}\right)−{b}}{\mathrm{3}{a}} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{34}}×\mathrm{cos}\:\mathrm{0}.\mathrm{5982}−\mathrm{2}}{\mathrm{3}×\mathrm{2}}=\frac{\sqrt{\mathrm{34}}×\mathrm{cos}\:\mathrm{0}.\mathrm{5982}−\mathrm{1}}{\mathrm{3}}=\mathrm{1}.\mathrm{272804} \\ $$$$ \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{2}\sqrt{\Delta}\mathrm{cos}\:\left(\frac{\mathrm{cos}^{−\mathrm{1}} {k}}{\mathrm{3}}−\frac{\mathrm{2}\pi}{\mathrm{3}}\right)−{b}}{\mathrm{3}{a}} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{34}}×\mathrm{cos}\:\left(−\mathrm{1}.\mathrm{496195}\right)−\mathrm{2}}{\mathrm{3}×\mathrm{2}}=\frac{\sqrt{\mathrm{34}}×\mathrm{cos}\:\left(−\mathrm{1}.\mathrm{496195}\right)−\mathrm{1}}{\mathrm{3}}=−\mathrm{0}.\mathrm{18847} \\ $$$$ \\ $$$${x}_{\mathrm{3}} =\frac{\mathrm{2}\sqrt{\Delta}\mathrm{cos}\:\left(\frac{\mathrm{cos}^{−\mathrm{1}} {k}}{\mathrm{3}}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)−{b}}{\mathrm{3}{a}} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{34}}×\mathrm{cos}\:\left(\mathrm{2}.\mathrm{692545}\right)−\mathrm{2}}{\mathrm{3}×\mathrm{2}}=\frac{\sqrt{\mathrm{34}}×\mathrm{cos}\:\left(\mathrm{2}.\mathrm{692545}\right)−\mathrm{1}}{\mathrm{3}}=−\mathrm{2}.\mathrm{084334} \\ $$$$ \\ $$
Commented by Saham last updated on 21/Feb/17
$$\mathrm{wow}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
