Question Number 10317 by Tawakalitu ayo mi last updated on 03/Feb/17
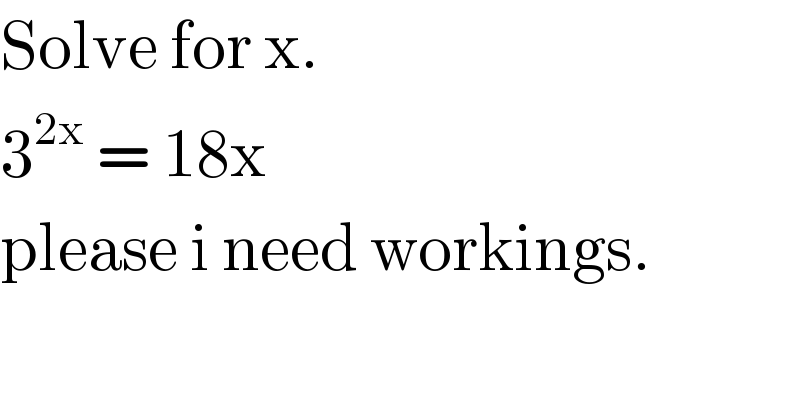
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}. \\ $$$$\mathrm{3}^{\mathrm{2x}} \:=\:\mathrm{18x} \\ $$$$\mathrm{please}\:\mathrm{i}\:\mathrm{need}\:\mathrm{workings}. \\ $$
Answered by mrW1 last updated on 03/Feb/17

$$\left(\mathrm{3}^{\mathrm{2}} \right)^{{x}} =\mathrm{18}{x} \\ $$$$\mathrm{9}^{{x}} =\mathrm{18}{x} \\ $$$${e}^{{x}\mathrm{ln}\:\mathrm{9}} =\mathrm{18}{x} \\ $$$$\mathrm{1}=\frac{\mathrm{18}}{−\mathrm{ln}\:\mathrm{9}}\left(−{x}\mathrm{ln}\:\mathrm{9}\right){e}^{−{x}\mathrm{ln}\:\mathrm{9}} \\ $$$$\left(−{x}\mathrm{ln}\:\mathrm{9}\right){e}^{−{x}\mathrm{ln}\:\mathrm{9}} =−\frac{\mathrm{ln}\:\mathrm{9}}{\mathrm{18}} \\ $$$$−{x}\mathrm{ln}\:\mathrm{9}={W}\left(−\frac{\mathrm{ln}\:\mathrm{9}}{\mathrm{18}}\right)\:{with}\:{W}={Lambert}\:{W}\:{function} \\ $$$${x}=−\frac{{W}\left(−\frac{\mathrm{ln}\:\mathrm{9}}{\mathrm{18}}\right)}{\mathrm{ln}\:\mathrm{9}}=−\frac{{W}\left(−\mathrm{0}.\mathrm{122068}\right)}{\mathrm{2}.\mathrm{197225}} \\ $$$$=\begin{cases}{−\frac{−\mathrm{0}.\mathrm{140479}}{\mathrm{2}.\mathrm{197225}}=\mathrm{0}.\mathrm{063935}}\\{−\frac{−\mathrm{3}.\mathrm{295837}}{\mathrm{2}.\mathrm{197225}}=\mathrm{1}.\mathrm{5}}\end{cases} \\ $$
Commented by Tawakalitu ayo mi last updated on 04/Feb/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by arge last updated on 04/Feb/17

$$ \\ $$$$ \\ $$$${log}\:\mathrm{3}^{\mathrm{2}{x}} ={log}\mathrm{18}{x} \\ $$$$\mathrm{2}{xlog}\:\mathrm{3}={log}\:\mathrm{18}+{log}\:{x} \\ $$$$ \\ $$$${log}\:{x}={y} \\ $$$$ \\ $$$$\mathrm{0}.\mathrm{95}{x}=\mathrm{1}.\mathrm{26}+{y} \\ $$$${x}=\frac{\mathrm{1}.\mathrm{26}+{y}}{\mathrm{0}.\mathrm{95}} \\ $$
