Question Number 77805 by Dah Solu Tion last updated on 10/Jan/20

$${Solve}\:{for}\:{x} \\ $$$$\frac{\mathrm{8}^{{x}} \:+\:\mathrm{27}^{{x}} }{\mathrm{12}^{{x}} \:+\:\mathrm{18}^{{x}} }\:=\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$
Answered by john santu last updated on 10/Jan/20
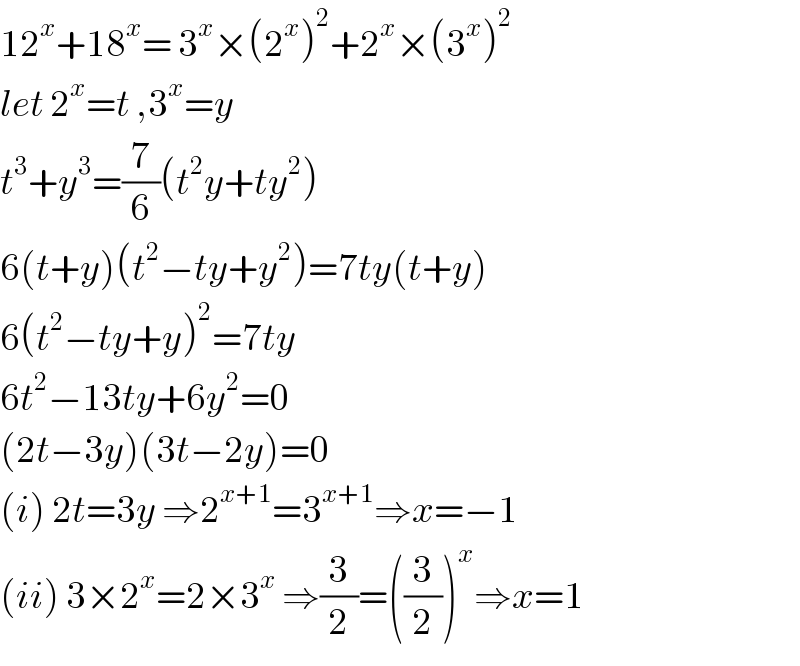
$$\mathrm{12}^{{x}} +\mathrm{18}^{{x}} =\:\mathrm{3}^{{x}} ×\left(\mathrm{2}^{{x}} \right)^{\mathrm{2}} +\mathrm{2}^{{x}} ×\left(\mathrm{3}^{{x}} \right)^{\mathrm{2}} \\ $$$${let}\:\mathrm{2}^{{x}} ={t}\:,\mathrm{3}^{{x}} ={y} \\ $$$${t}^{\mathrm{3}} +{y}^{\mathrm{3}} =\frac{\mathrm{7}}{\mathrm{6}}\left({t}^{\mathrm{2}} {y}+{ty}^{\mathrm{2}} \right) \\ $$$$\mathrm{6}\left({t}+{y}\right)\left({t}^{\mathrm{2}} −{ty}+{y}^{\mathrm{2}} \right)=\mathrm{7}{ty}\left({t}+{y}\right) \\ $$$$\mathrm{6}\left({t}^{\mathrm{2}} −{ty}+{y}\right)^{\mathrm{2}} =\mathrm{7}{ty} \\ $$$$\mathrm{6}{t}^{\mathrm{2}} −\mathrm{13}{ty}+\mathrm{6}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{2}{t}−\mathrm{3}{y}\right)\left(\mathrm{3}{t}−\mathrm{2}{y}\right)=\mathrm{0} \\ $$$$\left({i}\right)\:\mathrm{2}{t}=\mathrm{3}{y}\:\Rightarrow\mathrm{2}^{{x}+\mathrm{1}} =\mathrm{3}^{{x}+\mathrm{1}} \Rightarrow{x}=−\mathrm{1} \\ $$$$\left({ii}\right)\:\mathrm{3}×\mathrm{2}^{{x}} =\mathrm{2}×\mathrm{3}^{{x}} \:\Rightarrow\frac{\mathrm{3}}{\mathrm{2}}=\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{x}} \Rightarrow{x}=\mathrm{1} \\ $$
Commented by Dah Solu Tion last updated on 10/Jan/20

$${Thank}\:{boss} \\ $$
