Question Number 698 by 9999 last updated on 01/Mar/15
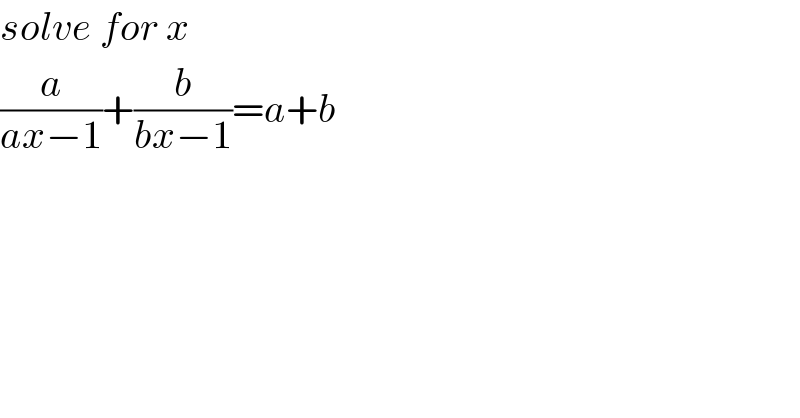
$${solve}\:{for}\:{x} \\ $$$$\frac{{a}}{{ax}−\mathrm{1}}+\frac{{b}}{{bx}−\mathrm{1}}={a}+{b} \\ $$
Commented by 123456 last updated on 28/Feb/15
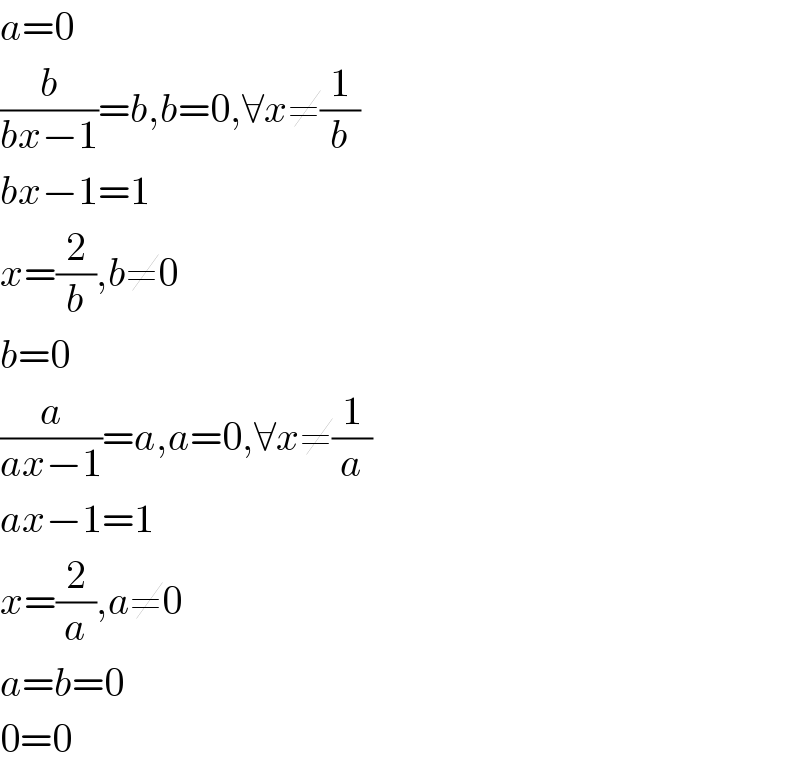
$${a}=\mathrm{0} \\ $$$$\frac{{b}}{{bx}−\mathrm{1}}={b},{b}=\mathrm{0},\forall{x}\neq\frac{\mathrm{1}}{{b}} \\ $$$${bx}−\mathrm{1}=\mathrm{1} \\ $$$${x}=\frac{\mathrm{2}}{{b}},{b}\neq\mathrm{0} \\ $$$${b}=\mathrm{0} \\ $$$$\frac{{a}}{{ax}−\mathrm{1}}={a},{a}=\mathrm{0},\forall{x}\neq\frac{\mathrm{1}}{{a}} \\ $$$${ax}−\mathrm{1}=\mathrm{1} \\ $$$${x}=\frac{\mathrm{2}}{{a}},{a}\neq\mathrm{0} \\ $$$${a}={b}=\mathrm{0} \\ $$$$\mathrm{0}=\mathrm{0} \\ $$
Answered by prakash jain last updated on 01/Mar/15
![(a/(ax−1))+(b/(bx−1))=a+b a(bx−1)+b(ax−1)=(a+b)(ax−1)(bx−1) 2abx−(a+b)=ab(a+b)x^2 −(a+b)^2 x+(a+b) ab(a+b)x^2 −2abx−(a+b)^2 x+2(a+b)=0 abx[(a+b)x−2]−(a+b)[(a+b)x−2]=0 [(a+b)x−2][abx−(a+b)]=0 x=(2/(a+b)) or x=((a+b)/(ab))](https://www.tinkutara.com/question/Q701.png)
$$\frac{{a}}{{ax}−\mathrm{1}}+\frac{{b}}{{bx}−\mathrm{1}}={a}+{b} \\ $$$${a}\left({bx}−\mathrm{1}\right)+{b}\left({ax}−\mathrm{1}\right)=\left({a}+{b}\right)\left({ax}−\mathrm{1}\right)\left({bx}−\mathrm{1}\right) \\ $$$$\mathrm{2}{abx}−\left({a}+{b}\right)={ab}\left({a}+{b}\right){x}^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{2}} {x}+\left({a}+{b}\right) \\ $$$${ab}\left({a}+{b}\right){x}^{\mathrm{2}} −\mathrm{2}{abx}−\left({a}+{b}\right)^{\mathrm{2}} {x}+\mathrm{2}\left({a}+{b}\right)=\mathrm{0} \\ $$$${abx}\left[\left({a}+{b}\right){x}−\mathrm{2}\right]−\left({a}+{b}\right)\left[\left({a}+{b}\right){x}−\mathrm{2}\right]=\mathrm{0} \\ $$$$\left[\left({a}+{b}\right){x}−\mathrm{2}\right]\left[{abx}−\left({a}+{b}\right)\right]=\mathrm{0} \\ $$$${x}=\frac{\mathrm{2}}{{a}+{b}}\:\mathrm{or}\:{x}=\frac{{a}+{b}}{{ab}} \\ $$
