Solve-for-x-and-y-2-x-3-y-31-equation-i-3-x-2-y-17-equation-ii-please-help-

Question Number 5924 by sanusihammed last updated on 05/Jun/16

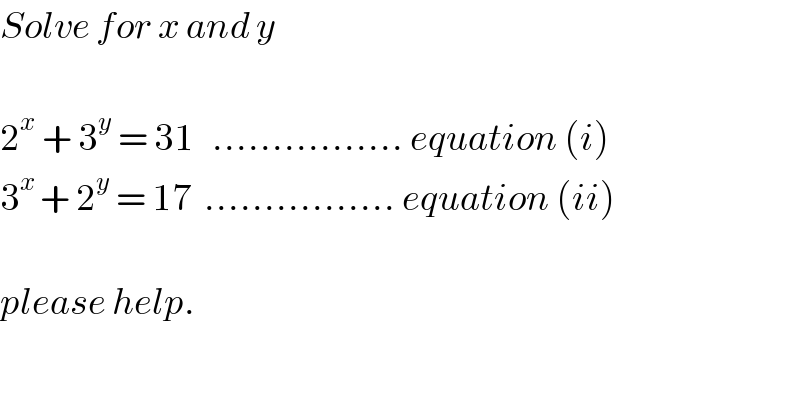
$${Solve}\:{for}\:{x}\:{and}\:{y} \\ $$$$ \\ $$$$\mathrm{2}^{{x}} \:+\:\mathrm{3}^{{y}} \:=\:\mathrm{31}\:\:\:…………….\:{equation}\:\left({i}\right) \\ $$$$\mathrm{3}^{{x}\:} +\:\mathrm{2}^{{y}} \:=\:\mathrm{17}\:\:…………….\:{equation}\:\left({ii}\right) \\ $$$$ \\ $$$${please}\:{help}. \\ $$$$ \\ $$

Commented by sanusihammed last updated on 05/Jun/16

$${please}\:{help} \\ $$

Commented by FilupSmith last updated on 05/Jun/16

we have seen your question. If no one replies it is often because we are thinking about how to solve it or we dont know how. I am not very good with these kinds of things, but I will keep thinking about it.

$$\mathrm{we}\:\mathrm{have}\:\mathrm{seen}\:\mathrm{your}\:\mathrm{question}. \\ $$$$\mathrm{If}\:\mathrm{no}\:\mathrm{one}\:\mathrm{replies}\:\mathrm{it}\:\mathrm{is}\:\mathrm{often}\:\mathrm{because} \\ $$$$\mathrm{we}\:\mathrm{are}\:\mathrm{thinking}\:\mathrm{about}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it} \\ $$$$\mathrm{or}\:\mathrm{we}\:\mathrm{dont}\:\mathrm{know}\:\mathrm{how}.\:\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{very}\:\mathrm{good} \\ $$$$\mathrm{with}\:\mathrm{these}\:\mathrm{kinds}\:\mathrm{of}\:\mathrm{things},\:\mathrm{but}\:\mathrm{I}\:\mathrm{will} \\ $$$$\mathrm{keep}\:\mathrm{thinking}\:\mathrm{about}\:\mathrm{it}. \\ $$

Commented by Yozzii last updated on 05/Jun/16

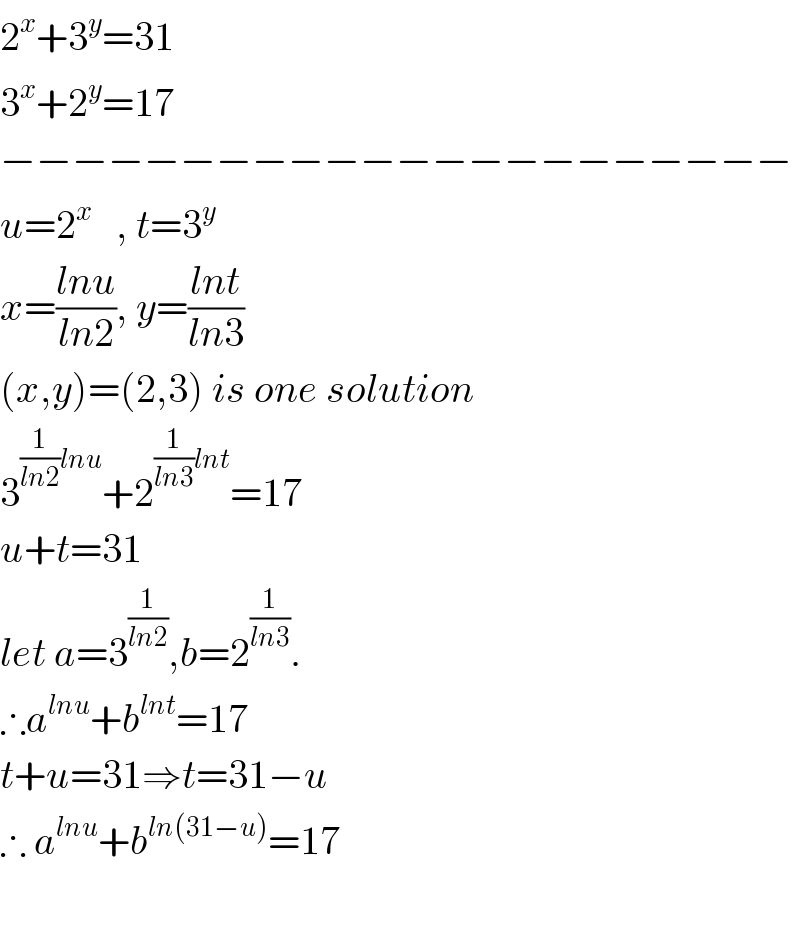
2^x +3^y =31 3^x +2^y =17 −−−−−−−−−−−−−−−−−−−−−− u=2^x , t=3^y x=((lnu)/(ln2)), y=((lnt)/(ln3)) (x,y)=(2,3) is one solution 3^((1/(ln2))lnu) +2^((1/(ln3))lnt) =17 u+t=31 let a=3^(1/(ln2)) ,b=2^(1/(ln3)) . ∴a^(lnu) +b^(lnt) =17 t+u=31⇒t=31−u ∴ a^(lnu) +b^(ln(31−u)) =17

$$\mathrm{2}^{{x}} +\mathrm{3}^{{y}} =\mathrm{31} \\ $$$$\mathrm{3}^{{x}} +\mathrm{2}^{{y}} =\mathrm{17} \\ $$$$−−−−−−−−−−−−−−−−−−−−−− \\ $$$${u}=\mathrm{2}^{{x}} \:\:\:,\:{t}=\mathrm{3}^{{y}} \\ $$$${x}=\frac{{lnu}}{{ln}\mathrm{2}},\:{y}=\frac{{lnt}}{{ln}\mathrm{3}} \\ $$$$\left({x},{y}\right)=\left(\mathrm{2},\mathrm{3}\right)\:{is}\:{one}\:{solution} \\ $$$$\mathrm{3}^{\frac{\mathrm{1}}{{ln}\mathrm{2}}{lnu}} +\mathrm{2}^{\frac{\mathrm{1}}{{ln}\mathrm{3}}{lnt}} =\mathrm{17} \\ $$$${u}+{t}=\mathrm{31} \\ $$$${let}\:{a}=\mathrm{3}^{\frac{\mathrm{1}}{{ln}\mathrm{2}}} ,{b}=\mathrm{2}^{\frac{\mathrm{1}}{{ln}\mathrm{3}}} . \\ $$$$\therefore{a}^{{lnu}} +{b}^{{lnt}} =\mathrm{17} \\ $$$${t}+{u}=\mathrm{31}\Rightarrow{t}=\mathrm{31}−{u} \\ $$$$\therefore\:{a}^{{lnu}} +{b}^{{ln}\left(\mathrm{31}−{u}\right)} =\mathrm{17} \\ $$$$ \\ $$

Commented by sanusihammed last updated on 05/Jun/16

$${Thanks}\:{so}\:{much} \\ $$

Commented by prakash jain last updated on 08/Jun/16

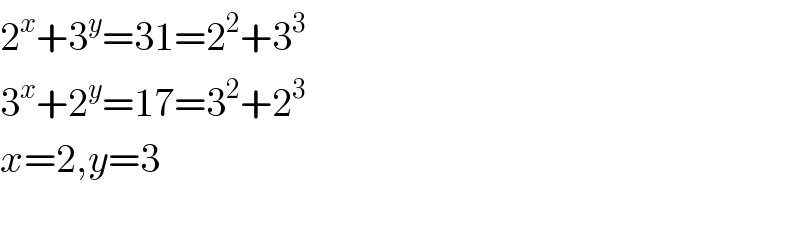
2^x +3^y =31=2^2 +3^3 3^x +2^y =17=3^2 +2^3 x=2,y=3

$$\mathrm{2}^{{x}} +\mathrm{3}^{{y}} =\mathrm{31}=\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} \\ $$$$\mathrm{3}^{{x}} +\mathrm{2}^{{y}} =\mathrm{17}=\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} \\ $$$${x}=\mathrm{2},{y}=\mathrm{3} \\ $$$$ \\ $$

Facebook Tweet Pin

Solve-for-x-and-y-2-x-3-y-31-equation-i-3-x-2-y-17-equation-ii-please-help-

Leave a Reply Cancel reply