solve-for-x-and-y-the-equation-2lnx-lny-ln-5x-6y-

Question Number 68899 by Rio Michael last updated on 16/Sep/19

$${solve}\:{for}\:{x}\:{and}\:{y}\:{the}\:{equation} \\ $$$$\:\mathrm{2}{lnx}\:−{lny}\:={ln}\left(\mathrm{5}{x}−\mathrm{6}{y}\right) \\ $$

Commented by kaivan.ahmadi last updated on 16/Sep/19

$${i}\:{dont}\:{know}.{i}\:{think}\:{it}\:{is}\:{hard}. \\ $$

Commented by Rio Michael last updated on 16/Sep/19

$${thanks}\:{sir} \\ $$

Commented by kaivan.ahmadi last updated on 16/Sep/19

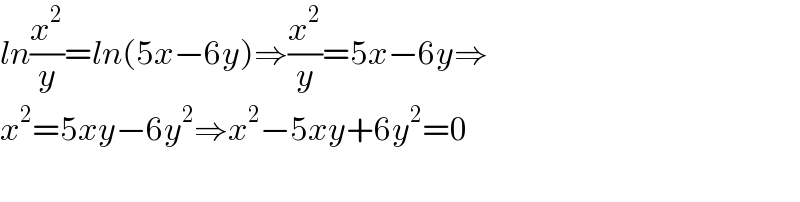
ln(x^2 /y)=ln(5x−6y)⇒(x^2 /y)=5x−6y⇒ x^2 =5xy−6y^2 ⇒x^2 −5xy+6y^2 =0

$${ln}\frac{{x}^{\mathrm{2}} }{{y}}={ln}\left(\mathrm{5}{x}−\mathrm{6}{y}\right)\Rightarrow\frac{{x}^{\mathrm{2}} }{{y}}=\mathrm{5}{x}−\mathrm{6}{y}\Rightarrow \\ $$$${x}^{\mathrm{2}} =\mathrm{5}{xy}−\mathrm{6}{y}^{\mathrm{2}} \Rightarrow{x}^{\mathrm{2}} −\mathrm{5}{xy}+\mathrm{6}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$

Commented by Rio Michael last updated on 16/Sep/19

x^2 −5xy +6y^2 =0 x(x−3y)−2y(x−3y)=0 (x−3y)(x−2y)=0 (x/y) = (3/1) or (x/y) = (2/1) x=3 ,y =1 or x=2 ,y=1

$${x}^{\mathrm{2}} −\mathrm{5}{xy}\:+\mathrm{6}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}\left({x}−\mathrm{3}{y}\right)−\mathrm{2}{y}\left({x}−\mathrm{3}{y}\right)=\mathrm{0} \\ $$$$\left({x}−\mathrm{3}{y}\right)\left({x}−\mathrm{2}{y}\right)=\mathrm{0} \\ $$$$\frac{{x}}{{y}}\:=\:\frac{\mathrm{3}}{\mathrm{1}}\:\:{or}\:\:\frac{{x}}{{y}}\:=\:\frac{\mathrm{2}}{\mathrm{1}} \\ $$$${x}=\mathrm{3}\:,{y}\:=\mathrm{1}\:{or}\:{x}=\mathrm{2}\:,{y}=\mathrm{1} \\ $$

Commented by kaivan.ahmadi last updated on 16/Sep/19

$${nice} \\ $$$$ \\ $$

Commented by Rio Michael last updated on 16/Sep/19

$${how}\:{about}\:{the}\:{next}\:{one}\:{sir} \\ $$

Commented by Rasheed.Sindhi last updated on 17/Sep/19

Rio Michael sir. x^2 −5xy +6y^2 =0 : I think that x & y couldn′t be determined uniquely by this single equation. (x/y) = (3/1)⇏x=3,y=1 (x/y) = (3/1)⇒x=3k,y=k ∀k∈C x^2 −5xy +6y^2 =0⇒(3k)^2 −5(3k)(k)+6(k)^2 =0 9k^2 −15k^2 +6k^2 =0⇒15k^2 −15k^2 =0⇒0=0

$$\mathrm{Rio}\:\mathrm{Michael}\:\mathrm{sir}. \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{xy}\:+\mathrm{6}{y}^{\mathrm{2}} =\mathrm{0}\::\:{I}\:{think}\:{that} \\ $$$${x}\:\&\:{y}\:{couldn}'{t}\:{be}\:{determined}\:{uniquely} \\ $$$${by}\:{this}\:{single}\:{equation}. \\ $$$$\frac{{x}}{{y}}\:=\:\frac{\mathrm{3}}{\mathrm{1}}\nRightarrow{x}=\mathrm{3},{y}=\mathrm{1} \\ $$$$\frac{{x}}{{y}}\:=\:\frac{\mathrm{3}}{\mathrm{1}}\Rightarrow{x}=\mathrm{3}{k},{y}={k}\:\forall{k}\in\mathbb{C} \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{xy}\:+\mathrm{6}{y}^{\mathrm{2}} =\mathrm{0}\Rightarrow\left(\mathrm{3}{k}\right)^{\mathrm{2}} −\mathrm{5}\left(\mathrm{3}{k}\right)\left({k}\right)+\mathrm{6}\left({k}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{9}{k}^{\mathrm{2}} −\mathrm{15}{k}^{\mathrm{2}} +\mathrm{6}{k}^{\mathrm{2}} =\mathrm{0}\Rightarrow\mathrm{15}{k}^{\mathrm{2}} −\mathrm{15}{k}^{\mathrm{2}} =\mathrm{0}\Rightarrow\mathrm{0}=\mathrm{0} \\ $$$$ \\ $$

Commented by kaivan.ahmadi last updated on 17/Sep/19

$${thank}\:{sir},\:{its}\:{general} \\ $$

Commented by Rio Michael last updated on 21/Sep/19

$${so}\:{sir}\:{the}\:{question}\:{is}\:{wrong}? \\ $$

Facebook Tweet Pin

solve-for-x-and-y-the-equation-2lnx-lny-ln-5x-6y-

Leave a Reply Cancel reply