Question Number 10360 by Tawakalitu ayo mi last updated on 05/Feb/17
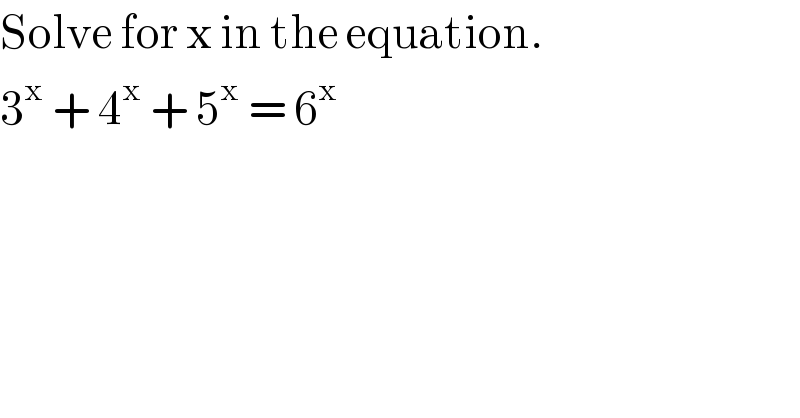
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}\:\mathrm{in}\:\mathrm{the}\:\mathrm{equation}. \\ $$$$\mathrm{3}^{\mathrm{x}} \:+\:\mathrm{4}^{\mathrm{x}} \:+\:\mathrm{5}^{\mathrm{x}} \:=\:\mathrm{6}^{\mathrm{x}} \\ $$
Answered by mrW1 last updated on 05/Feb/17

$${when}\:{x}=\mathrm{2}, \\ $$$$\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} =\mathrm{9}+\mathrm{16}+\mathrm{25}=\mathrm{50} \\ $$$$\mathrm{6}^{\mathrm{2}} =\mathrm{36} \\ $$$${i}.{e}.\:\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} >\mathrm{6}^{\mathrm{2}} \\ $$$$ \\ $$$${when}\:{x}=\mathrm{4}, \\ $$$$\mathrm{3}^{\mathrm{4}} +\mathrm{4}^{\mathrm{4}} +\mathrm{5}^{\mathrm{4}} =\mathrm{81}+\mathrm{256}+\mathrm{625}=\mathrm{962} \\ $$$$\mathrm{6}^{\mathrm{4}} =\mathrm{1296} \\ $$$${i}.{e}.\:\mathrm{3}^{\mathrm{4}} +\mathrm{4}^{\mathrm{4}} +\mathrm{5}^{\mathrm{4}} <\mathrm{6}^{\mathrm{4}} \\ $$$$ \\ $$$$\Rightarrow{the}\:{solution}\:{is}\:{between}\:\mathrm{2}\:{and}\:\mathrm{4}. \\ $$$$ \\ $$$${through}\:{try}\:{and}\:{error}\:{we}\:{get}\:{the} \\ $$$${solution}\:{x}=\mathrm{3}: \\ $$$$\mathrm{3}^{\mathrm{3}} +\mathrm{4}^{\mathrm{3}} +\mathrm{5}^{\mathrm{3}} =\mathrm{27}+\mathrm{64}+\mathrm{125}=\mathrm{216} \\ $$$$\mathrm{6}^{\mathrm{3}} =\mathrm{216} \\ $$
Commented by mrW1 last updated on 05/Feb/17

$${I}'{m}\:{not}\:{sure}\:{if}\:{there}\:{is}\:{an}\:{analytical} \\ $$$${solution}\:{to}\:{this}\:{question}. \\ $$
Commented by Tawakalitu ayo mi last updated on 05/Feb/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by arge last updated on 05/Feb/17
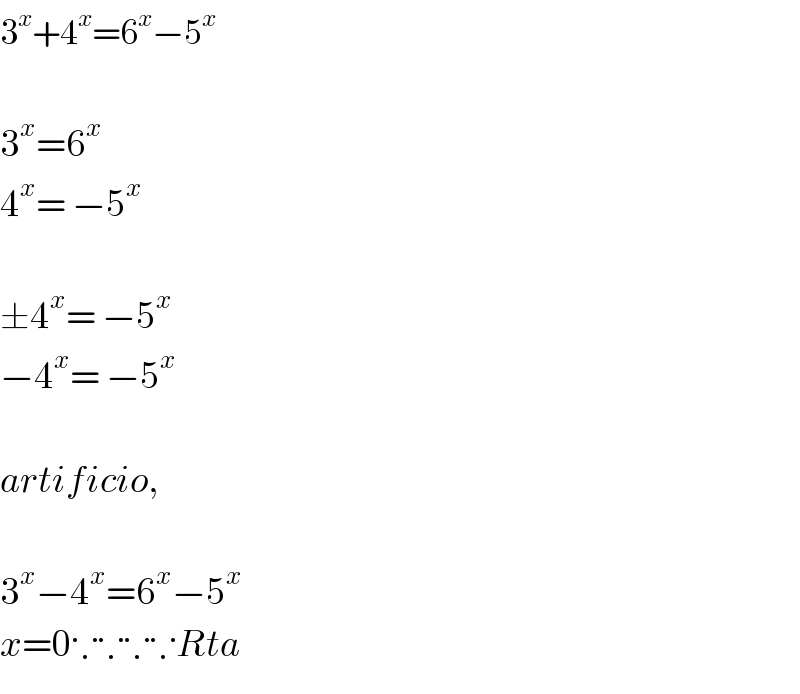
$$\mathrm{3}^{{x}} +\mathrm{4}^{{x}} =\mathrm{6}^{{x}} −\mathrm{5}^{{x}} \\ $$$$ \\ $$$$\mathrm{3}^{{x}} =\mathrm{6}^{{x}} \\ $$$$\mathrm{4}^{{x}} =\:−\mathrm{5}^{{x}} \\ $$$$ \\ $$$$\pm\mathrm{4}^{{x}} =\:−\mathrm{5}^{{x}} \\ $$$$−\mathrm{4}^{{x}} =\:−\mathrm{5}^{{x}} \\ $$$$ \\ $$$${artificio}, \\ $$$$ \\ $$$$\mathrm{3}^{{x}} −\mathrm{4}^{{x}} =\mathrm{6}^{{x}} −\mathrm{5}^{{x}} \\ $$$${x}=\mathrm{0}\because\because\because\because{Rta} \\ $$
Commented by FilupSmith last updated on 06/Feb/17

$$\mathrm{if}\:{x}=\mathrm{0},\:\mathrm{3}=\mathrm{1} \\ $$
Answered by chux last updated on 06/Feb/17

$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\mathrm{i}\:\mathrm{think}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{by}\:\mathrm{linear}\:\mathrm{approximation} \\ $$$$ \\ $$$$\left(\mathrm{1}+\mathrm{2}\right)^{\mathrm{x}} +\left(\mathrm{1}+\mathrm{3}\right)^{\mathrm{x}} +\left(\mathrm{1}+\mathrm{4}\right)^{\mathrm{x}} =\left(\mathrm{1}+\mathrm{5}\right)^{\mathrm{x}} \\ $$
