Question Number 7054 by Tawakalitu. last updated on 08/Aug/16
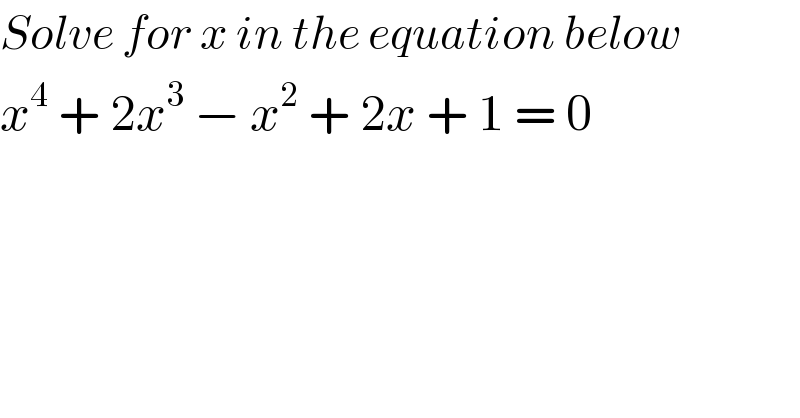
$${Solve}\:{for}\:{x}\:{in}\:{the}\:{equation}\:{below} \\ $$$${x}^{\mathrm{4}} \:+\:\mathrm{2}{x}^{\mathrm{3}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{2}{x}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$ \\ $$
Commented by prakash jain last updated on 08/Aug/16

$$\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} ={x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{x}^{\mathrm{3}} +\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1} \\ $$$${given}\:{expr}−\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} =−\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$ \\ $$$$\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} ={x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} \\ $$$$={x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1} \\ $$$${given}\:{expr}−\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=−\mathrm{4}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}=−\mathrm{4}{x}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right) \\ $$$${hence}\:{given}\:{expr} \\ $$$$=\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{x}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right) \\ $$$$=\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}\right) \\ $$$${can}\:{be}\:{solved}\:{as}\:{quadratic} \\ $$
Commented by Tawakalitu. last updated on 08/Aug/16
$${Thanks}\:{so}\:{much}.\:{i}\:{appreciate} \\ $$
