Menu Close

Solve-for-x-y-x-y-R-x-3-3xy-2-46-i-3x-2-y-y-3-9-ii-

Tinku Tara 0 Comments
Pin




Question Number 9424 by tawakalitu last updated on 07/Dec/16
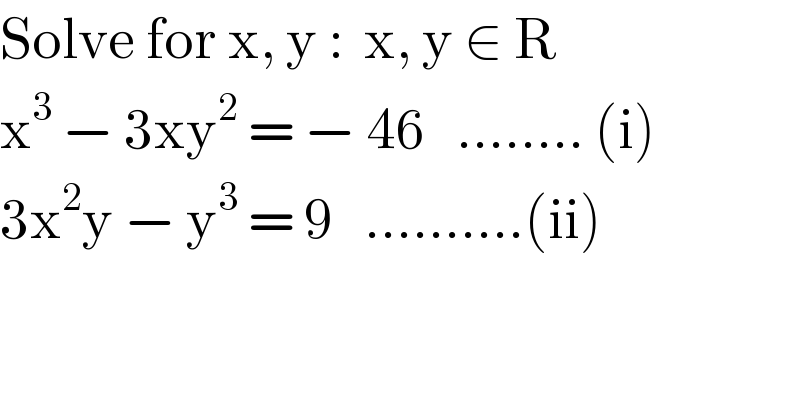
Solve for x, y : x, y ∈ R x^3 − 3xy^2 = − 46 ........ (i) 3x^2 y − y^3 = 9 ..........(ii)
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x},\:\mathrm{y}\::\:\:\mathrm{x},\:\mathrm{y}\:\in\:\mathrm{R} \\ $$$$\mathrm{x}^{\mathrm{3}} \:−\:\mathrm{3xy}^{\mathrm{2}} \:=\:−\:\mathrm{46}\:\:\:……..\:\left(\mathrm{i}\right) \\ $$$$\mathrm{3x}^{\mathrm{2}} \mathrm{y}\:−\:\mathrm{y}^{\mathrm{3}} \:=\:\mathrm{9}\:\:\:……….\left(\mathrm{ii}\right) \\ $$
Answered by mrW last updated on 07/Dec/16
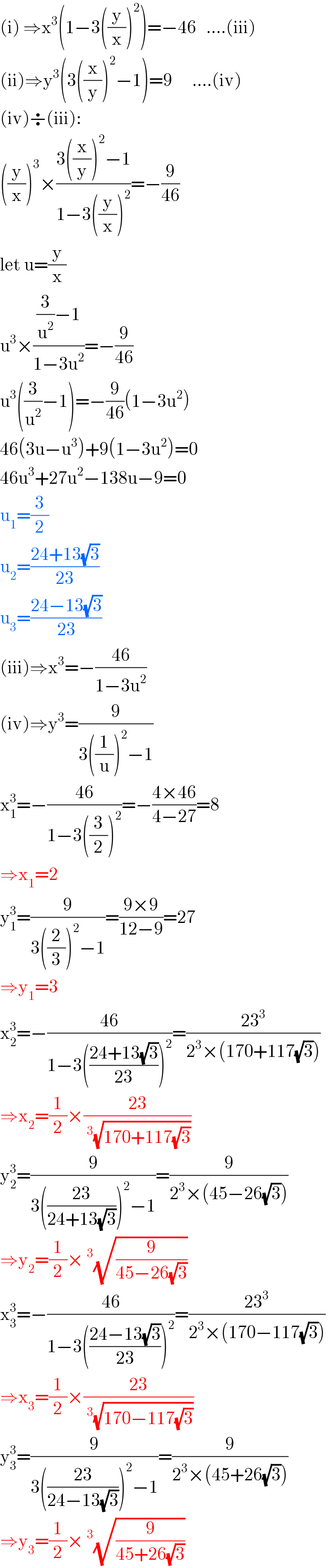
(i) ⇒x^3 (1−3((y/x))^2 )=−46 ....(iii) (ii)⇒y^3 (3((x/y))^2 −1)=9 ....(iv) (iv)÷(iii): ((y/x))^3 ×((3((x/y))^2 −1)/(1−3((y/x))^2 ))=−(9/(46)) let u=(y/x) u^3 ×(((3/u^2 )−1)/(1−3u^2 ))=−(9/(46)) u^3 ((3/u^2 )−1)=−(9/(46))(1−3u^2 ) 46(3u−u^3 )+9(1−3u^2 )=0 46u^3 +27u^2 −138u−9=0 u_1 =(3/2) u_2 =((24+13(√3))/(23)) u_3 =((24−13(√3))/(23)) (iii)⇒x^3 =−((46)/(1−3u^2 )) (iv)⇒y^3 =(9/(3((1/u))^2 −1)) x_1 ^3 =−((46)/(1−3((3/2))^2 ))=−((4×46)/(4−27))=8 ⇒x_1 =2 y_1 ^3 =(9/(3((2/3))^2 −1))=((9×9)/(12−9))=27 ⇒y_1 =3 x_2 ^3 =−((46)/(1−3(((24+13(√3))/(23)))^2 ))=((23^3 )/(2^3 ×(170+117(√3)))) ⇒x_2 =(1/2)×((23)/(^3 (√(170+117(√3))))) y_2 ^3 =(9/(3(((23)/(24+13(√3))))^2 −1))=(9/(2^3 ×(45−26(√3)))) ⇒y_2 =(1/2)×^3 (√(9/(45−26(√3)))) x_3 ^3 =−((46)/(1−3(((24−13(√3))/(23)))^2 ))=((23^3 )/(2^3 ×(170−117(√3)))) ⇒x_3 =(1/2)×((23)/(^3 (√(170−117(√3))))) y_3 ^3 =(9/(3(((23)/(24−13(√3))))^2 −1))=(9/(2^3 ×(45+26(√3)))) ⇒y_3 =(1/2)×^3 (√(9/(45+26(√3))))
$$\left(\mathrm{i}\right)\:\Rightarrow\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{3}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^{\mathrm{2}} \right)=−\mathrm{46}\:\:\:….\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\mathrm{y}^{\mathrm{3}} \left(\mathrm{3}\left(\frac{\mathrm{x}}{\mathrm{y}}\right)^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{9}\:\:\:\:\:\:….\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{iv}\right)\boldsymbol{\div}\left(\mathrm{iii}\right): \\ $$$$\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^{\mathrm{3}} ×\frac{\mathrm{3}\left(\frac{\mathrm{x}}{\mathrm{y}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}−\mathrm{3}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^{\mathrm{2}} }=−\frac{\mathrm{9}}{\mathrm{46}} \\ $$$$\mathrm{let}\:\mathrm{u}=\frac{\mathrm{y}}{\mathrm{x}} \\ $$$$\mathrm{u}^{\mathrm{3}} ×\frac{\frac{\mathrm{3}}{\mathrm{u}^{\mathrm{2}} }−\mathrm{1}}{\mathrm{1}−\mathrm{3u}^{\mathrm{2}} }=−\frac{\mathrm{9}}{\mathrm{46}} \\ $$$$\mathrm{u}^{\mathrm{3}} \left(\frac{\mathrm{3}}{\mathrm{u}^{\mathrm{2}} }−\mathrm{1}\right)=−\frac{\mathrm{9}}{\mathrm{46}}\left(\mathrm{1}−\mathrm{3u}^{\mathrm{2}} \right) \\ $$$$\mathrm{46}\left(\mathrm{3u}−\mathrm{u}^{\mathrm{3}} \right)+\mathrm{9}\left(\mathrm{1}−\mathrm{3u}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{46u}^{\mathrm{3}} +\mathrm{27u}^{\mathrm{2}} −\mathrm{138u}−\mathrm{9}=\mathrm{0} \\ $$$$\mathrm{u}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{u}_{\mathrm{2}} =\frac{\mathrm{24}+\mathrm{13}\sqrt{\mathrm{3}}}{\mathrm{23}} \\ $$$$\mathrm{u}_{\mathrm{3}} =\frac{\mathrm{24}−\mathrm{13}\sqrt{\mathrm{3}}}{\mathrm{23}} \\ $$$$\left(\mathrm{iii}\right)\Rightarrow\mathrm{x}^{\mathrm{3}} =−\frac{\mathrm{46}}{\mathrm{1}−\mathrm{3u}^{\mathrm{2}} } \\ $$$$\left(\mathrm{iv}\right)\Rightarrow\mathrm{y}^{\mathrm{3}} =\frac{\mathrm{9}}{\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{x}_{\mathrm{1}} ^{\mathrm{3}} =−\frac{\mathrm{46}}{\mathrm{1}−\mathrm{3}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }=−\frac{\mathrm{4}×\mathrm{46}}{\mathrm{4}−\mathrm{27}}=\mathrm{8} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{1}} =\mathrm{2} \\ $$$$\mathrm{y}_{\mathrm{1}} ^{\mathrm{3}} =\frac{\mathrm{9}}{\mathrm{3}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{9}×\mathrm{9}}{\mathrm{12}−\mathrm{9}}=\mathrm{27} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{1}} =\mathrm{3} \\ $$$$\mathrm{x}_{\mathrm{2}} ^{\mathrm{3}} =−\frac{\mathrm{46}}{\mathrm{1}−\mathrm{3}\left(\frac{\mathrm{24}+\mathrm{13}\sqrt{\mathrm{3}}}{\mathrm{23}}\right)^{\mathrm{2}} }=\frac{\mathrm{23}^{\mathrm{3}} }{\mathrm{2}^{\mathrm{3}} ×\left(\mathrm{170}+\mathrm{117}\sqrt{\mathrm{3}}\right)} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{23}}{\:^{\mathrm{3}} \sqrt{\mathrm{170}+\mathrm{117}\sqrt{\mathrm{3}}}} \\ $$$$\mathrm{y}_{\mathrm{2}} ^{\mathrm{3}} =\frac{\mathrm{9}}{\mathrm{3}\left(\frac{\mathrm{23}}{\mathrm{24}+\mathrm{13}\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{9}}{\mathrm{2}^{\mathrm{3}} ×\left(\mathrm{45}−\mathrm{26}\sqrt{\mathrm{3}}\right)} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\:^{\mathrm{3}} \sqrt{\frac{\mathrm{9}}{\mathrm{45}−\mathrm{26}\sqrt{\mathrm{3}}}} \\ $$$$\mathrm{x}_{\mathrm{3}} ^{\mathrm{3}} =−\frac{\mathrm{46}}{\mathrm{1}−\mathrm{3}\left(\frac{\mathrm{24}−\mathrm{13}\sqrt{\mathrm{3}}}{\mathrm{23}}\right)^{\mathrm{2}} }=\frac{\mathrm{23}^{\mathrm{3}} }{\mathrm{2}^{\mathrm{3}} ×\left(\mathrm{170}−\mathrm{117}\sqrt{\mathrm{3}}\right)} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{23}}{\:^{\mathrm{3}} \sqrt{\mathrm{170}−\mathrm{117}\sqrt{\mathrm{3}}}} \\ $$$$\mathrm{y}_{\mathrm{3}} ^{\mathrm{3}} =\frac{\mathrm{9}}{\mathrm{3}\left(\frac{\mathrm{23}}{\mathrm{24}−\mathrm{13}\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{9}}{\mathrm{2}^{\mathrm{3}} ×\left(\mathrm{45}+\mathrm{26}\sqrt{\mathrm{3}}\right)} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}×\:^{\mathrm{3}} \sqrt{\frac{\mathrm{9}}{\mathrm{45}+\mathrm{26}\sqrt{\mathrm{3}}}} \\ $$
Commented by tawakalitu last updated on 07/Dec/16
Thank you sir. God bless you.
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *