Question Number 67349 by Joel122 last updated on 26/Aug/19
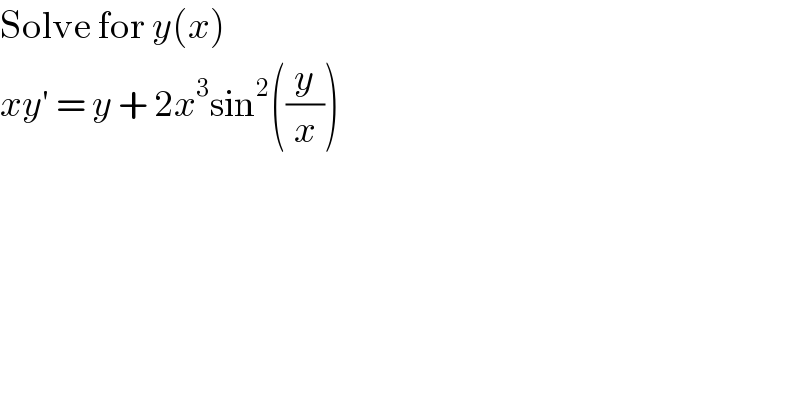
$$\mathrm{Solve}\:\mathrm{for}\:{y}\left({x}\right) \\ $$$${xy}'\:=\:{y}\:+\:\mathrm{2}{x}^{\mathrm{3}} \mathrm{sin}^{\mathrm{2}} \left(\frac{{y}}{{x}}\right) \\ $$
Answered by mind is power last updated on 26/Aug/19
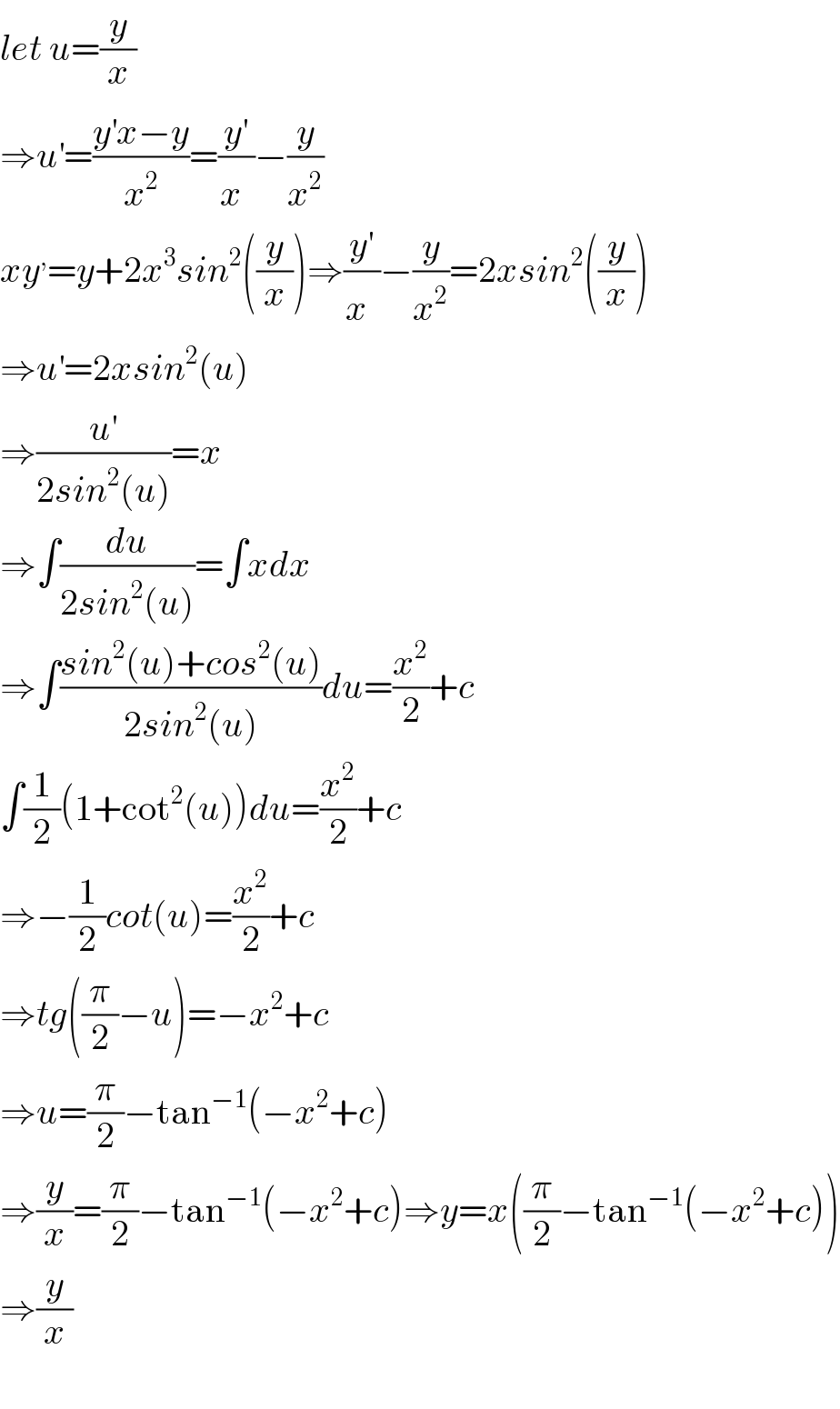
$${let}\:{u}=\frac{{y}}{{x}} \\ $$$$\Rightarrow{u}^{'} =\frac{{y}^{'} {x}−{y}}{{x}^{\mathrm{2}} }=\frac{{y}^{'} }{{x}^{} }−\frac{{y}}{{x}^{\mathrm{2}} } \\ $$$${xy}^{,} ={y}+\mathrm{2}{x}^{\mathrm{3}} {sin}^{\mathrm{2}} \left(\frac{{y}}{{x}}\right)\Rightarrow\frac{{y}'}{{x}^{} }−\frac{{y}}{{x}^{\mathrm{2}} }=\mathrm{2}{xsin}^{\mathrm{2}} \left(\frac{{y}}{{x}}\right) \\ $$$$\Rightarrow{u}^{'} =\mathrm{2}{xsin}^{\mathrm{2}} \left({u}\right) \\ $$$$\Rightarrow\frac{{u}^{'} }{\mathrm{2}{sin}^{\mathrm{2}} \left({u}\right)}={x} \\ $$$$\Rightarrow\int\frac{{du}}{\mathrm{2}{sin}^{\mathrm{2}} \left({u}\right)}=\int{xdx} \\ $$$$\Rightarrow\int\frac{{sin}^{\mathrm{2}} \left({u}\right)+{cos}^{\mathrm{2}} \left({u}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left({u}\right)}{du}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{c} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cot}^{\mathrm{2}} \left({u}\right)\right){du}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{c} \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\mathrm{2}}{cot}\left({u}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{c} \\ $$$$\Rightarrow{tg}\left(\frac{\pi}{\mathrm{2}}−{u}\right)=−{x}^{\mathrm{2}} +{c} \\ $$$$\Rightarrow{u}=\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(−{x}^{\mathrm{2}} +{c}\right) \\ $$$$\Rightarrow\frac{{y}}{{x}}=\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(−{x}^{\mathrm{2}} +{c}\right)\Rightarrow{y}={x}\left(\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(−{x}^{\mathrm{2}} +{c}\right)\right) \\ $$$$\Rightarrow\frac{{y}}{{x}} \\ $$$$ \\ $$
Commented by Joel122 last updated on 26/Aug/19
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by mind is power last updated on 26/Aug/19

$${y}'{re}\:{welcom} \\ $$
