Question Number 76439 by mathocean1 last updated on 27/Dec/19

$$\mathrm{solve}\:\mathrm{in}\:\left[\mathrm{0};\mathrm{2}\pi\left[\:\right.\right. \\ $$$$\mathrm{1}+\mathrm{2sin3}{x}\leqslant\mathrm{0} \\ $$
Answered by john santu last updated on 27/Dec/19
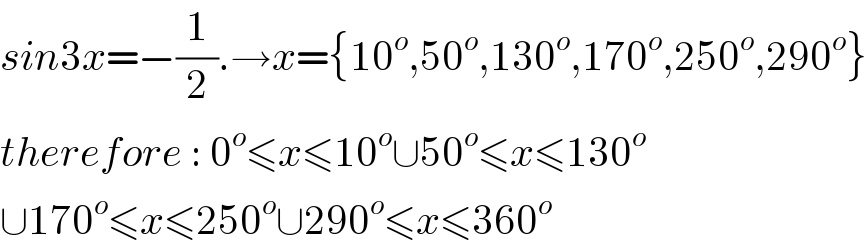
$${sin}\mathrm{3}{x}=−\frac{\mathrm{1}}{\mathrm{2}}.\rightarrow{x}=\left\{\mathrm{10}^{{o}} ,\mathrm{50}^{{o}} ,\mathrm{130}^{{o}} ,\mathrm{170}^{{o}} ,\mathrm{250}^{{o}} ,\mathrm{290}^{{o}} \right\} \\ $$$${therefore}\::\:\mathrm{0}^{{o}} \leqslant{x}\leqslant\mathrm{10}^{{o}} \cup\mathrm{50}^{{o}} \leqslant{x}\leqslant\mathrm{130}^{{o}} \\ $$$$\cup\mathrm{170}^{{o}} \leqslant{x}\leqslant\mathrm{250}^{{o}} \cup\mathrm{290}^{{o}} \leqslant{x}\leqslant\mathrm{360}^{{o}} \\ $$
