solve-in-0-pi-sinx-sin-3-x-1-cos2x-

Question Number 77041 by mathocean1 last updated on 02/Jan/20

solve in [0; π]

\sin x - \sin^{3} x = 1 - \cos 2 x

Answered by mind is power last updated on 02/Jan/20

\Leftrightarrow

1

\sin (x) (1 - \sin^{2} (x)) = {2 \sin}^{2} (x)

\Leftrightarrow \sin (x) (\sin^{2} (x) + 2 \sin (x) - 1) = 0

easy Know

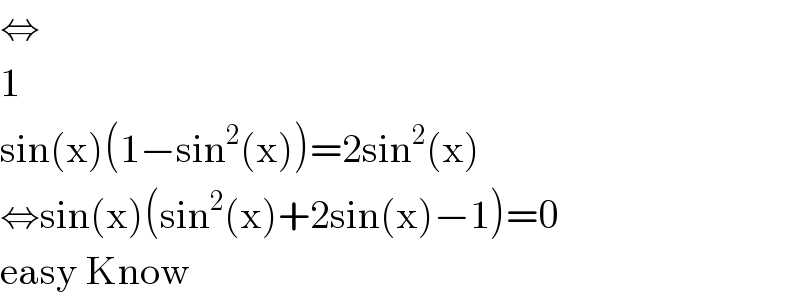
Answered by mr W last updated on 02/Jan/20

\sin x - \sin^{3} x = 1 - \cos 2 x

\sin x - \sin^{3} x = 1 - 1 + 2 \sin^{2} x

\sin x - \sin^{3} x - 2 \sin^{2} x = 0

\sin x (1 - 2 \sin x - \sin^{2} x) = 0

\Rightarrow \sin x = 0 \Rightarrow x = 0, π

\Rightarrow \sin x = \sqrt{2} - 1 \Rightarrow x = \sin^{- 1} (\sqrt{2} - 1), π - \sin^{- 1} (\sqrt{2} - 1)

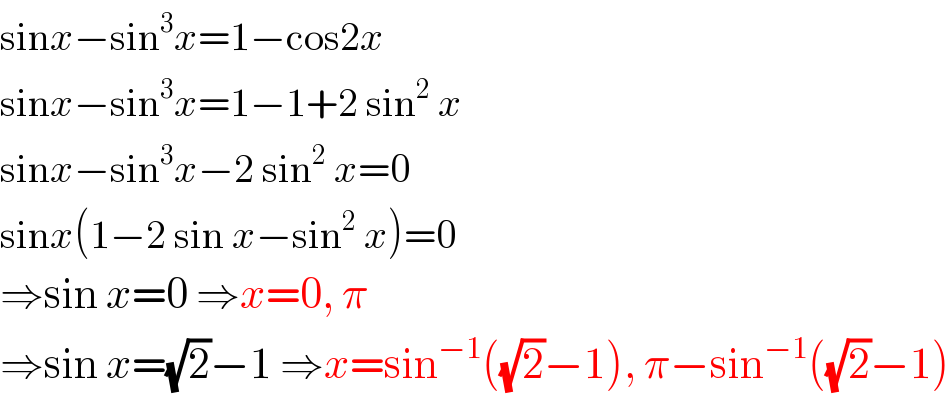
Commented by mr W last updated on 02/Jan/20

D e a r s i r! H a p p y n e w y e a r t o y o u t o o!

Commented by mind is power last updated on 02/Jan/20

Hello Mr How are You sir ? happy new year

Commented by mathocean1 last updated on 03/Jan/20

thank you sirs