Question Number 135435 by physicstutes last updated on 13/Mar/21
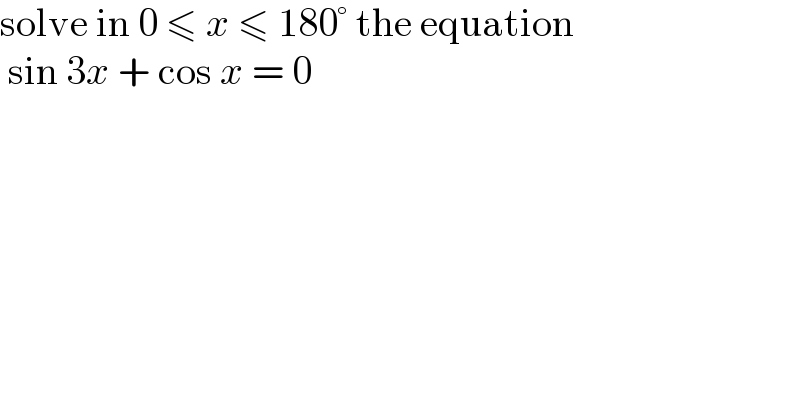
$$\mathrm{solve}\:\mathrm{in}\:\mathrm{0}\:\leqslant\:{x}\:\leqslant\:\mathrm{180}°\:\mathrm{the}\:\mathrm{equation} \\ $$$$\:\mathrm{sin}\:\mathrm{3}{x}\:+\:\mathrm{cos}\:{x}\:=\:\mathrm{0}\: \\ $$
Answered by mr W last updated on 13/Mar/21
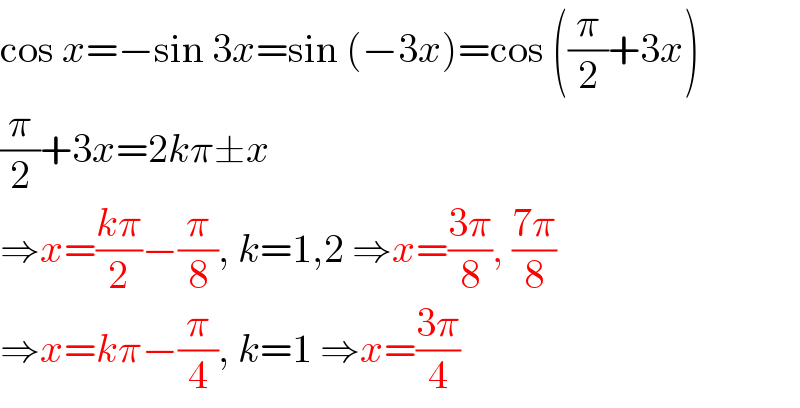
$$\mathrm{cos}\:{x}=−\mathrm{sin}\:\mathrm{3}{x}=\mathrm{sin}\:\left(−\mathrm{3}{x}\right)=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}+\mathrm{3}{x}\right) \\ $$$$\frac{\pi}{\mathrm{2}}+\mathrm{3}{x}=\mathrm{2}{k}\pi\pm{x} \\ $$$$\Rightarrow{x}=\frac{{k}\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{8}},\:{k}=\mathrm{1},\mathrm{2}\:\Rightarrow{x}=\frac{\mathrm{3}\pi}{\mathrm{8}},\:\frac{\mathrm{7}\pi}{\mathrm{8}} \\ $$$$\Rightarrow{x}={k}\pi−\frac{\pi}{\mathrm{4}},\:{k}=\mathrm{1}\:\Rightarrow{x}=\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$
Commented by physicstutes last updated on 13/Mar/21

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
