Question Number 67189 by mathmax by abdo last updated on 23/Aug/19

$${solve}\:{inside}\:{R}^{\mathrm{3}} \:{the}\:{system}\:\begin{cases}{\mathrm{2}{x}+{y}+{z}\:=\mathrm{1}}\\{{x}+\mathrm{2}{y}+{z}\:=\mathrm{2}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{x}+{y}+\mathrm{2}{z}\:=\mathrm{3}\right. \\ $$
Answered by MJS last updated on 23/Aug/19
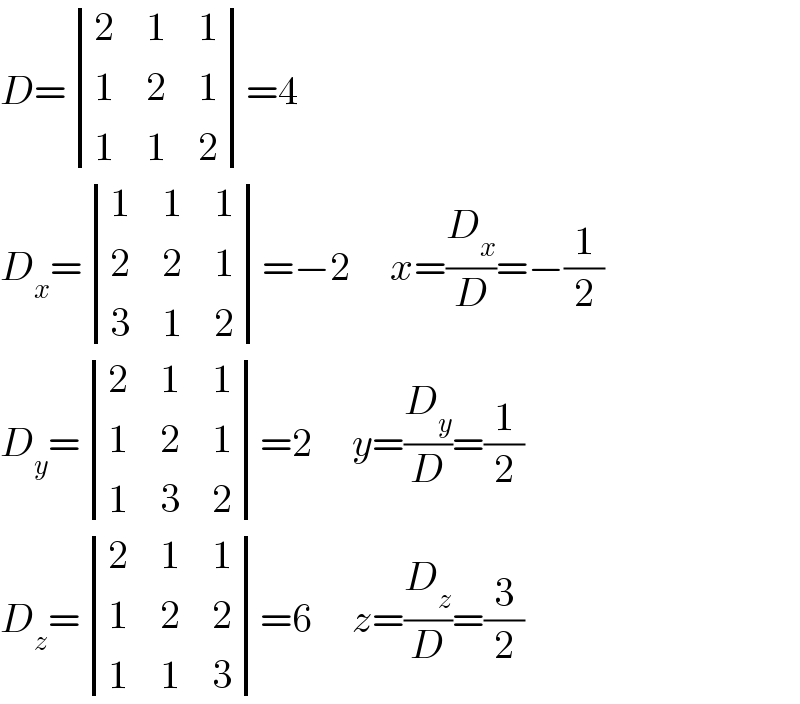
$${D}=\begin{vmatrix}{\mathrm{2}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{2}}\end{vmatrix}=\mathrm{4} \\ $$$${D}_{{x}} =\begin{vmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{2}}&{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{3}}&{\mathrm{1}}&{\mathrm{2}}\end{vmatrix}=−\mathrm{2}\:\:\:\:\:{x}=\frac{{D}_{{x}} }{{D}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${D}_{{y}} =\begin{vmatrix}{\mathrm{2}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{3}}&{\mathrm{2}}\end{vmatrix}=\mathrm{2}\:\:\:\:\:{y}=\frac{{D}_{{y}} }{{D}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${D}_{{z}} =\begin{vmatrix}{\mathrm{2}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{2}}\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{3}}\end{vmatrix}=\mathrm{6}\:\:\:\:\:{z}=\frac{{D}_{{z}} }{{D}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by turbo msup by abdo last updated on 24/Aug/19
$${thank}\:{you}\:{sir}\:{mjs}. \\ $$
