Question Number 5866 by sanusihammed last updated on 02/Jun/16
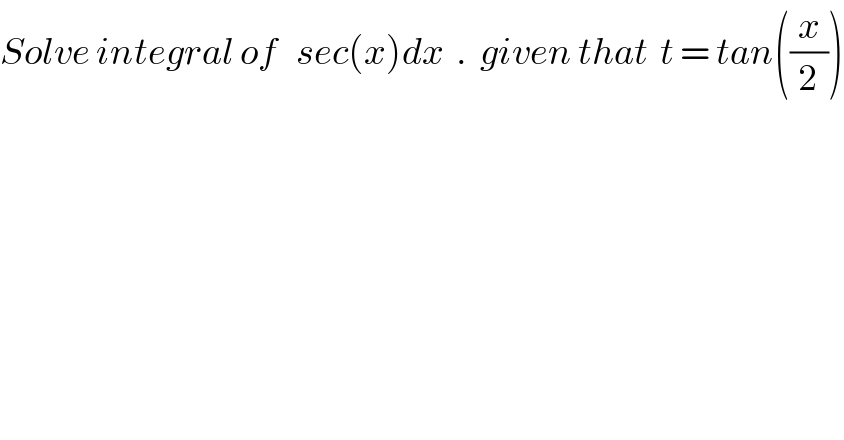
$${Solve}\:{integral}\:{of}\:\:\:{sec}\left({x}\right){dx}\:\:.\:\:{given}\:{that}\:\:{t}\:=\:{tan}\left(\frac{{x}}{\mathrm{2}}\right) \\ $$
Answered by Yozzii last updated on 02/Jun/16
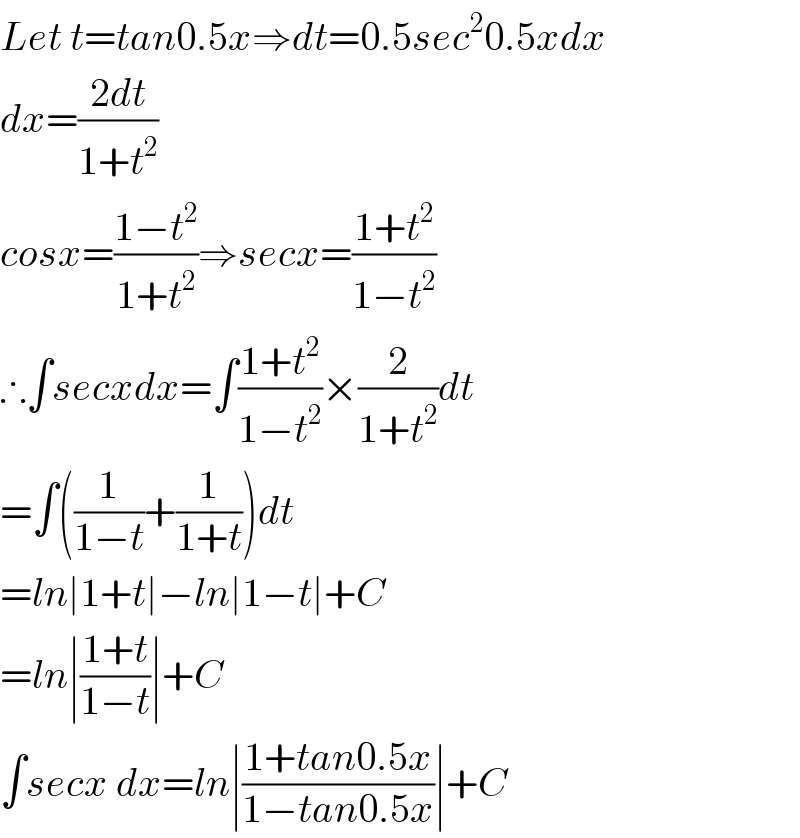
$${Let}\:{t}={tan}\mathrm{0}.\mathrm{5}{x}\Rightarrow{dt}=\mathrm{0}.\mathrm{5}{sec}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{xdx} \\ $$$${dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${cosx}=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\Rightarrow{secx}=\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\therefore\int{secxdx}=\int\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} }×\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\int\left(\frac{\mathrm{1}}{\mathrm{1}−{t}}+\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt} \\ $$$$={ln}\mid\mathrm{1}+{t}\mid−{ln}\mid\mathrm{1}−{t}\mid+{C} \\ $$$$={ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid+{C} \\ $$$$\int{secx}\:{dx}={ln}\mid\frac{\mathrm{1}+{tan}\mathrm{0}.\mathrm{5}{x}}{\mathrm{1}−{tan}\mathrm{0}.\mathrm{5}{x}}\mid+{C} \\ $$
Commented by sanusihammed last updated on 02/Jun/16
$${Interesting}\:\:{thanks}. \\ $$
