Menu Close

Solve-simultaneously-2x-y-2z-0-i-7x-6y-9z-0-ii-x-3-y-3-z-3-1728-iii-

Tinku Tara 0 Comments
Pin




Question Number 8885 by tawakalitu last updated on 03/Nov/16
Solve simultaneously 2x + y − 2z = 0 ......... (i) 7x + 6y − 9z = 0 ....... (ii) x^3 + y^3 + z^3 = 1728 ...... (iii)
$$\mathrm{Solve}\:\mathrm{simultaneously} \\ $$$$ \\ $$$$\mathrm{2x}\:+\:\mathrm{y}\:−\:\mathrm{2z}\:=\:\mathrm{0}\:………\:\left(\mathrm{i}\right) \\ $$$$\mathrm{7x}\:+\:\mathrm{6y}\:−\:\mathrm{9z}\:=\:\mathrm{0}\:…….\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{y}^{\mathrm{3}} \:+\:\mathrm{z}^{\mathrm{3}} \:=\:\mathrm{1728}\:\:\:\:……\:\left(\mathrm{iii}\right) \\ $$
Answered by Rasheed Soomro last updated on 04/Nov/16
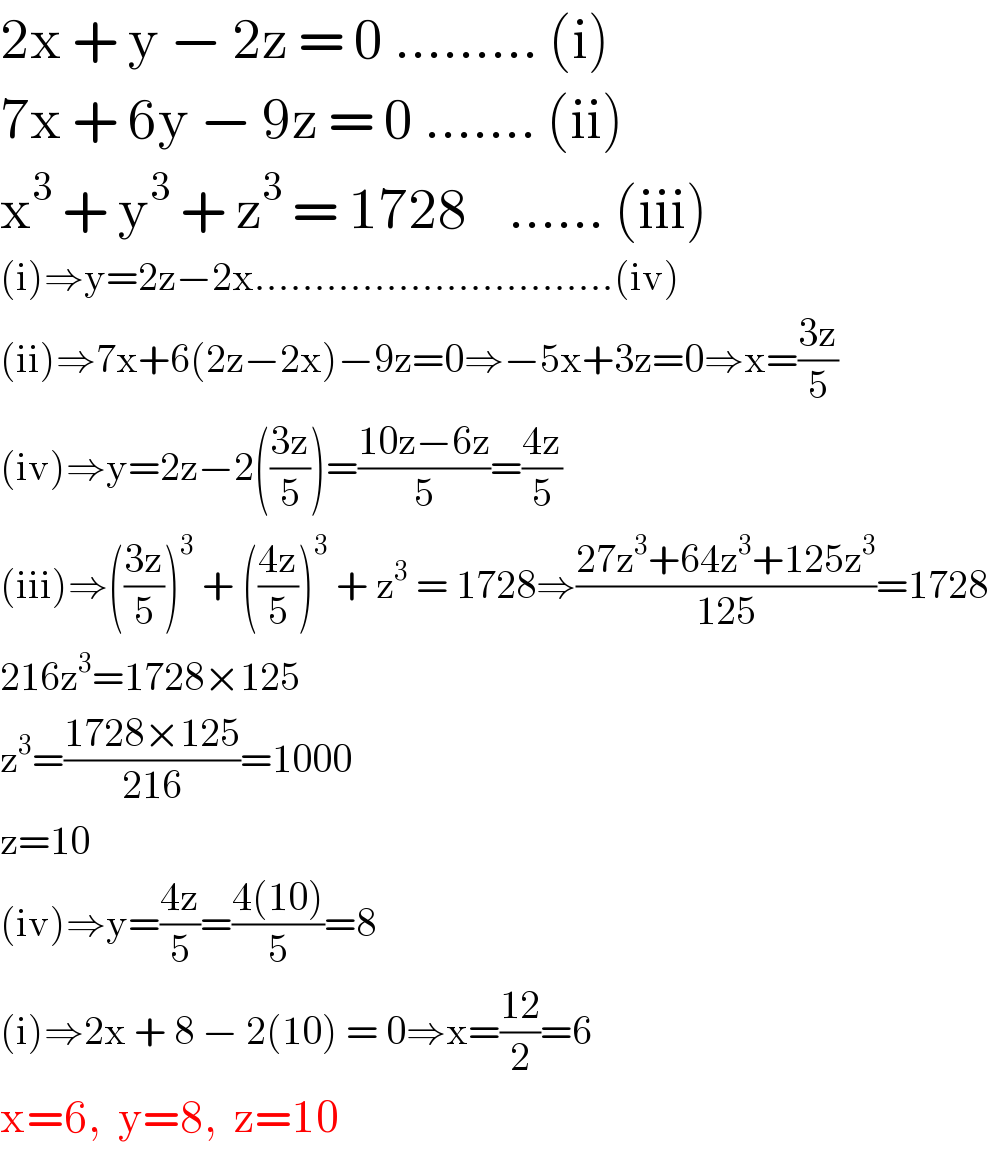
2x + y − 2z = 0 ......... (i) 7x + 6y − 9z = 0 ....... (ii) x^3 + y^3 + z^3 = 1728 ...... (iii) (i)⇒y=2z−2x..............................(iv) (ii)⇒7x+6(2z−2x)−9z=0⇒−5x+3z=0⇒x=((3z)/5) (iv)⇒y=2z−2(((3z)/5))=((10z−6z)/5)=((4z)/5) (iii)⇒(((3z)/5))^3 + (((4z)/5))^3 + z^3 = 1728⇒((27z^3 +64z^3 +125z^3 )/(125))=1728 216z^3 =1728×125 z^3 =((1728×125)/(216))=1000 z=10 (iv)⇒y=((4z)/5)=((4(10))/5)=8 (i)⇒2x + 8 − 2(10) = 0⇒x=((12)/2)=6 x=6, y=8, z=10
$$\mathrm{2x}\:+\:\mathrm{y}\:−\:\mathrm{2z}\:=\:\mathrm{0}\:………\:\left(\mathrm{i}\right) \\ $$$$\mathrm{7x}\:+\:\mathrm{6y}\:−\:\mathrm{9z}\:=\:\mathrm{0}\:…….\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{y}^{\mathrm{3}} \:+\:\mathrm{z}^{\mathrm{3}} \:=\:\mathrm{1728}\:\:\:\:……\:\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{i}\right)\Rightarrow\mathrm{y}=\mathrm{2z}−\mathrm{2x}…………………………\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\mathrm{7x}+\mathrm{6}\left(\mathrm{2z}−\mathrm{2x}\right)−\mathrm{9z}=\mathrm{0}\Rightarrow−\mathrm{5x}+\mathrm{3z}=\mathrm{0}\Rightarrow\mathrm{x}=\frac{\mathrm{3z}}{\mathrm{5}} \\ $$$$\left(\mathrm{iv}\right)\Rightarrow\mathrm{y}=\mathrm{2z}−\mathrm{2}\left(\frac{\mathrm{3z}}{\mathrm{5}}\right)=\frac{\mathrm{10z}−\mathrm{6z}}{\mathrm{5}}=\frac{\mathrm{4z}}{\mathrm{5}} \\ $$$$\left(\mathrm{iii}\right)\Rightarrow\left(\frac{\mathrm{3z}}{\mathrm{5}}\right)^{\mathrm{3}} \:+\:\left(\frac{\mathrm{4z}}{\mathrm{5}}\right)^{\mathrm{3}} \:+\:\mathrm{z}^{\mathrm{3}} \:=\:\mathrm{1728}\Rightarrow\frac{\mathrm{27z}^{\mathrm{3}} +\mathrm{64z}^{\mathrm{3}} +\mathrm{125z}^{\mathrm{3}} }{\mathrm{125}}=\mathrm{1728} \\ $$$$\mathrm{216z}^{\mathrm{3}} =\mathrm{1728}×\mathrm{125} \\ $$$$\mathrm{z}^{\mathrm{3}} =\frac{\mathrm{1728}×\mathrm{125}}{\mathrm{216}}=\mathrm{1000} \\ $$$$\mathrm{z}=\mathrm{10} \\ $$$$\left(\mathrm{iv}\right)\Rightarrow\mathrm{y}=\frac{\mathrm{4z}}{\mathrm{5}}=\frac{\mathrm{4}\left(\mathrm{10}\right)}{\mathrm{5}}=\mathrm{8} \\ $$$$\left(\mathrm{i}\right)\Rightarrow\mathrm{2x}\:+\:\mathrm{8}\:−\:\mathrm{2}\left(\mathrm{10}\right)\:=\:\mathrm{0}\Rightarrow\mathrm{x}=\frac{\mathrm{12}}{\mathrm{2}}=\mathrm{6} \\ $$$$\mathrm{x}=\mathrm{6},\:\:\mathrm{y}=\mathrm{8},\:\:\mathrm{z}=\mathrm{10} \\ $$
Commented by tawakalitu last updated on 04/Nov/16
Thanks so much sir.
$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *