Question Number 9236 by tawakalitu last updated on 24/Nov/16
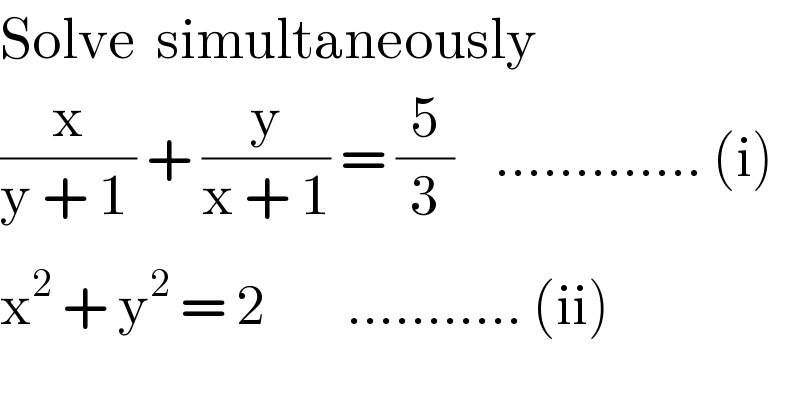
Answered by RasheedSoomro last updated on 25/Nov/16
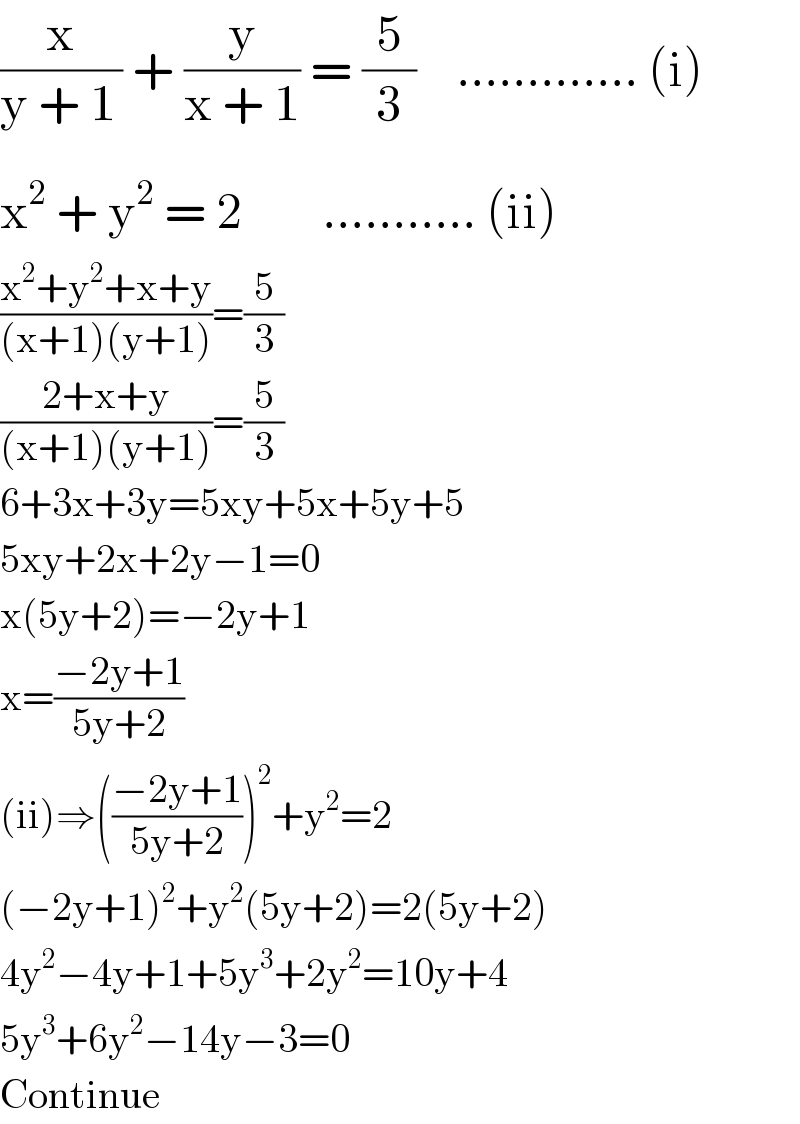
Commented by tawakalitu last updated on 25/Nov/16

Answered by RasheedSoomro last updated on 26/Nov/16
![(x/(y+1))+(y/(x+1))=(5/3) [x≠−1,y≠−1] x^2 +y^2 =2 −−−−−−−−− Let x+1=X, y+1=Y (i)⇒((X−1)/Y)+((Y−1)/X)=(5/3) [X≠0 , Y≠0] X^2 −X+Y^2 −Y=(5/3)XY X^2 +Y^2 −(X+Y)=(5/3)XY (ii)⇒(X−1)^2 +(Y−1)^2 =2 X^2 −2X+1+Y^2 −2Y+1=2 X^2 +Y^2 −2(X+Y)=0 X+Y=((X^2 +Y^2 )/2) X^2 +Y^2 −(X+Y)=(5/3)XY ⇒ X^2 +Y^2 −((X^2 +Y^2 )/2)=(5/3)XY 6X^2 +6Y^2 −3X^2 −3Y^2 =10XY 3X^2 −10XY+3Y^2 =0 3X^2 −XY−9XY+3Y^2 =0 X(3X−Y)−3Y(3X−Y)=0 (3X−Y)(X−3Y)=0 3X=Y ∣ X=3Y Case-1 Y=3X X+Y=((X^2 +Y^2 )/2)⇒X+3X=((X^2 +(3X)^2 )/2) 8X=10X^2 4X=5X^2 4X−5X^2 =0 [Dividing by X, as X≠0] 4−5X=0 X=(4/5) X+Y=((X^2 +Y^2 )/2) ⇒(4/5)+Y=(((4/5)^2 +Y^2 )/2) ⇒8+10Y=5(((16)/(25))+Y^2 )=((16)/5)+5Y^2 ⇒40+50Y=16+25Y^2 ⇒25Y^2 −50Y−24=0 ⇒Y=((50±(√(50^2 −4(25)(−24))))/(2(25)))=((50±70)/(50)) ⇒Y=2(2/5) ∣ Y=−(2/5) Solution set for (X,Y):{((4/5),2(2/5)),((4/5),− (2/5))} As x=X−1 , y=Y−1 , so Solution set for (x,y):{(−(1/5),1(2/5)),(−(1/5),− (7/5))} BUT (− (1/5),− (7/5)) doesn′t satisfy one of the given equations. S it′s an extraneous root. Hence the solution set is {(−(1/5),1(2/5))} By Case-2 it can be seen that (1(2/5),− (1/5)) is also a solution. Finally {(−(1/5),1(2/5)), (1(2/5),− (1/5))} is solution set.](https://www.tinkutara.com/question/Q9253.png)
Commented by tawakalitu last updated on 26/Nov/16