Solve-simultaneously-x-y-xy-3-i-x-1-y-1-4-ii-

Question Number 12023 by tawa last updated on 09/Apr/17

Solve simultaneously

x + y - \sqrt{xy} = 3 \dots \dots \dots . (i)

\sqrt{x + 1} + \sqrt{y + 1} = 4 \dots \dots \dots . (ii)

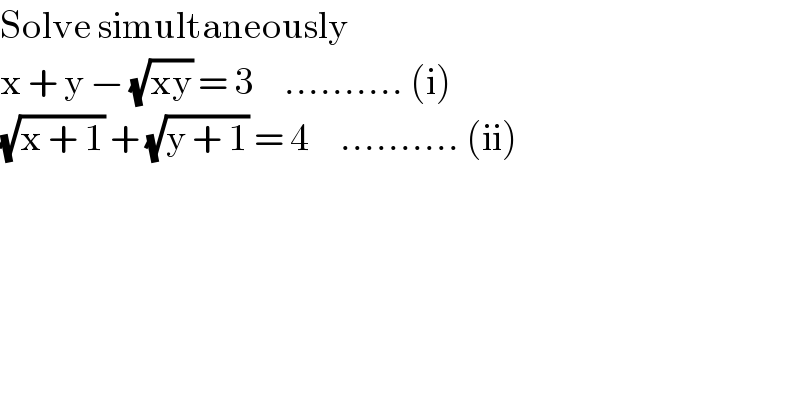
Answered by Mr Chheang Chantria last updated on 10/Apr/17

(i) . x + y - \sqrt{x y} ⩾ x + y - \frac{x + y}{2} = \frac{x + y}{2}

3 ⩾ \frac{x + y}{2}

\Leftrightarrow x + y ⩽ 6

. \sqrt{x + 1} + \sqrt{y + 1} ⩽ \sqrt{2 (x + y + 2)}

⩽ \sqrt{2 (6 + 2)} = 4

\Rightarrow \sqrt{x + 1} + \sqrt{y + 1} ⩽ 4

b y (i i) t h e s i g n e q u a l w h e n x = y = 3

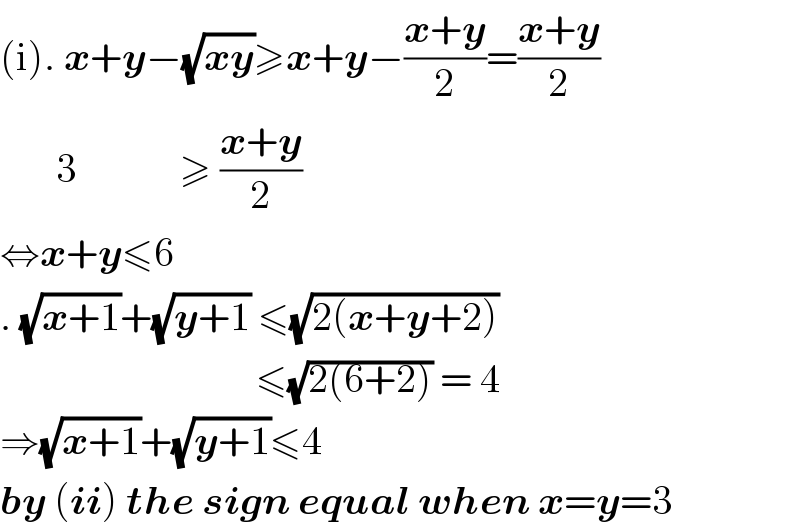
Commented by Mr Chheang Chantria last updated on 10/Apr/17

t h i s i s f o r s t u d e n t .

w e h a v e {(\sqrt{x} - \sqrt{y})}^{2} ⩾ 0 for x, y ⩾ 0

x - 2 \sqrt{x y} + y ⩾ 0

x + y ⩾ 2 \sqrt{x y}

o r \frac{x + y}{2} ⩾ \sqrt{x y}

o r - \frac{x + y}{2} ⩽ - \sqrt{x y}

Commented by tawa last updated on 10/Apr/17

God bless you sir .

Answered by ajfour last updated on 09/Apr/17

s q u a r i n g \dots (i i)

x + y + 2 + 2 \sqrt{(x + 2) (y + 1)} = 16

3 + \sqrt{x y} + 2 + 2 \sqrt{(x + 1) (y + 1)} = 16

2 \sqrt{(x + 1) (y + 1)} = 11 - \sqrt{x y}

s q u a r i n g :

4 (x y + 1 + x + y) = 121 + x y - 22 \sqrt{x y}

4 (x y + 1 + 3 + \sqrt{x y} = 121 + x y - 22 \sqrt{x y}

3 x y + 26 \sqrt{x y} - 105 = 0

i f \sqrt{x y} = t

3 t^{2} + 26 t - 105 = 0

t = \sqrt{x y} = \frac{- 26 + \sqrt{676 + 1260}}{6}

\sqrt{x y} = \frac{- 26 + 44}{6} = 3 \dots . (i i i)

x y = 9

f r o m \dots . (i)

x + y = 3 + \sqrt{x y}

\Rightarrow x + y = 6 \dots . (i v)

{(x - y)}^{2} = {(x + y)}^{2} - 4 x y

s o, {(x - y)}^{2} = 36 - 4 (9) = 0

\Rightarrow x = y

a n d a s x + y = 6

x = y = 3 .

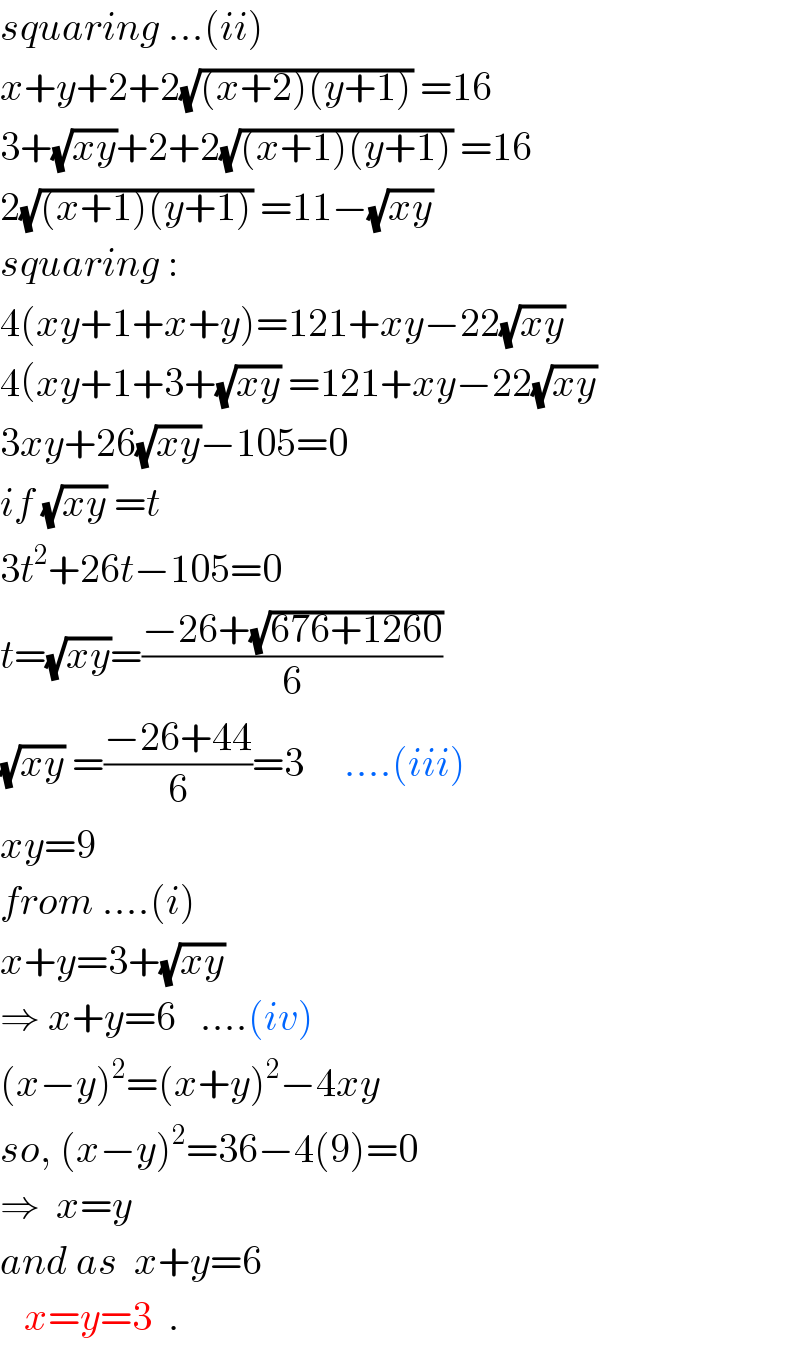
Commented by tawa last updated on 09/Apr/17

wow . God bless you sir .

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 09/Apr/17

x + 1 + y + 1 + 2 \sqrt{x + 1} \sqrt{y + 1} = 16

\sqrt{x y} + 5 + 2 \sqrt{x + 1} \sqrt{y + 1} = 16

2 \sqrt{x + 1} \sqrt{y + 1} = 11 - \sqrt{x y}

4 (x y + x + y + 1) = 121 - 22 \sqrt{x y} + x y

x + y = t

4 [{(t - 3)}^{2} + t + 1] = 121 - 22 (t - 3) + {(t - 3)}^{2}

3 {(t - 3)}^{2} + 26 (t - 3) - 105 = 0

t - 3 = \frac{- 26 \pm \sqrt{26^{2} + 4 \times 3 \times 105}}{2 \times 3} = \frac{- 26 \pm 44}{6} = 3, - 11.66

t = x + y = 6 \Rightarrow \sqrt{x y} = 3 \Rightarrow x y = 9

\Rightarrow x = y = 3

Commented by tawa last updated on 09/Apr/17

God bless you sir .

Facebook Tweet Pin