Question Number 77959 by john santu last updated on 12/Jan/20
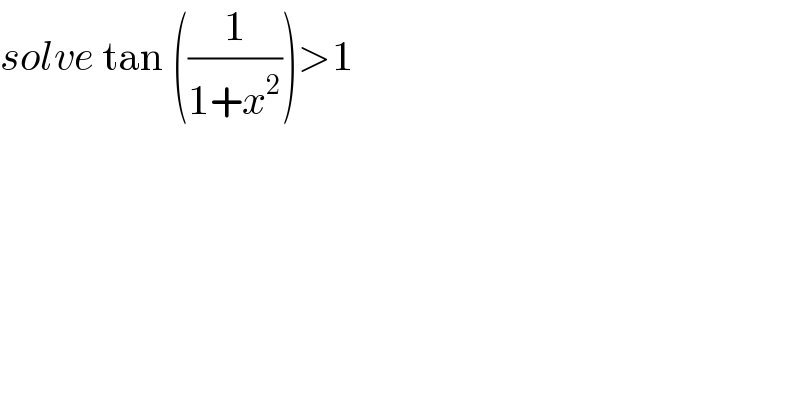
$${solve}\:\mathrm{tan}\:\left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)>\mathrm{1}\: \\ $$
Answered by mr W last updated on 12/Jan/20
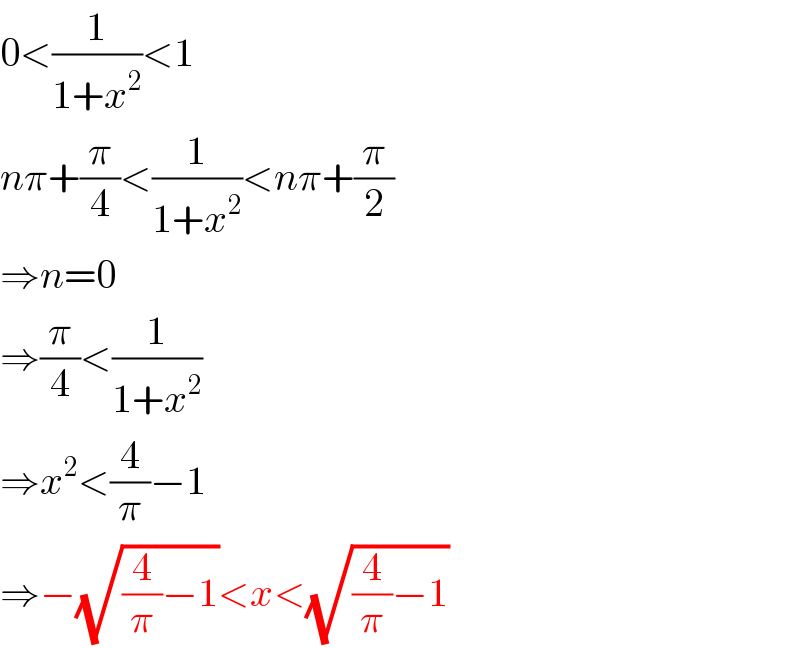
$$\mathrm{0}<\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }<\mathrm{1} \\ $$$${n}\pi+\frac{\pi}{\mathrm{4}}<\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }<{n}\pi+\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{n}=\mathrm{0} \\ $$$$\Rightarrow\frac{\pi}{\mathrm{4}}<\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{x}^{\mathrm{2}} <\frac{\mathrm{4}}{\pi}−\mathrm{1} \\ $$$$\Rightarrow−\sqrt{\frac{\mathrm{4}}{\pi}−\mathrm{1}}<{x}<\sqrt{\frac{\mathrm{4}}{\pi}−\mathrm{1}} \\ $$
Commented by john santu last updated on 12/Jan/20

$${thank}\:{you} \\ $$
Answered by MJS last updated on 12/Jan/20

$$\mathrm{tan}\:\alpha\:>\mathrm{1}\:\Rightarrow\:\frac{\pi}{\mathrm{4}}+{n}\pi<\alpha<\frac{\pi}{\mathrm{2}}+{n}\pi;\:{n}\in\mathbb{Z} \\ $$$$\frac{\pi}{\mathrm{4}}+{n}\pi<\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}<\frac{\pi}{\mathrm{2}}+{n}\pi \\ $$$$\frac{\mathrm{2}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}−\mathrm{1}<{x}^{\mathrm{2}} <\frac{\mathrm{4}}{\left(\mathrm{4}{n}+\mathrm{1}\right)\pi}−\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{upper}\:\mathrm{border}\:\mathrm{must}\:\mathrm{be}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{zero} \\ $$$$\frac{\mathrm{4}}{\left(\mathrm{4}{n}+\mathrm{1}\right)\pi}−\mathrm{1}>\mathrm{0}\:\Rightarrow\:{n}=\mathrm{0} \\ $$$$\mathrm{but}\:\frac{\mathrm{2}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}−\mathrm{1}<\mathrm{0}\wedge{x}^{\mathrm{2}} \geqslant\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{0}\leqslant{x}^{\mathrm{2}} <\frac{\mathrm{4}}{\pi}−\mathrm{1} \\ $$$$\Rightarrow\:−\sqrt{\frac{\mathrm{4}}{\pi}−\mathrm{1}}<{x}<+\sqrt{\frac{\mathrm{4}}{\pi}−\mathrm{1}} \\ $$
Commented by john santu last updated on 12/Jan/20

$${thank}\:{you} \\ $$
