Question Number 67380 by mathmax by abdo last updated on 26/Aug/19
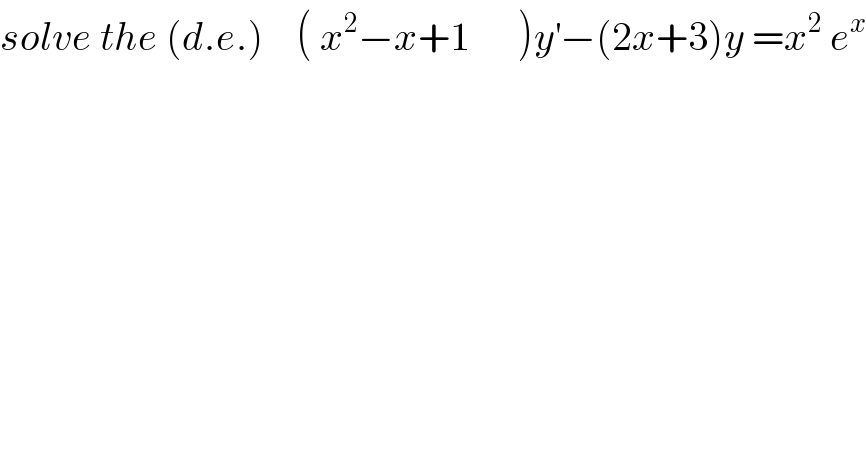
$${solve}\:{the}\:\left({d}.{e}.\right)\:\:\:\:\left(\:{x}^{\mathrm{2}} −{x}+\mathrm{1}\:\:\:\:\:\:\right){y}^{'} −\left(\mathrm{2}{x}+\mathrm{3}\right){y}\:={x}^{\mathrm{2}} \:{e}^{{x}} \\ $$
Commented by mathmax by abdo last updated on 28/Aug/19

$$\left({he}\right)\:\rightarrow\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right){y}^{'} −\left(\mathrm{2}{x}+\mathrm{3}\right){y}\:=\mathrm{0}\:\Rightarrow\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right){y}^{'} =\left(\mathrm{2}{x}+\mathrm{3}\right){y}\:\Rightarrow \\ $$$$\frac{{y}^{'} }{{y}}\:=\frac{\mathrm{2}{x}+\mathrm{3}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:\Rightarrow{ln}\mid{y}\mid\:=\int\:\:\frac{\mathrm{2}{x}+\mathrm{3}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:+{c}\:\:{but} \\ $$$$\int\:\:\frac{\mathrm{2}{x}+\mathrm{3}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}\:=\int\:\frac{\mathrm{2}{x}−\mathrm{1}\:+\mathrm{4}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:=\int\:\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:{dx}\:+\mathrm{4}\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}} \\ $$$$\int\:\:\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:={ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\:+{c}_{\mathrm{1}} \\ $$$$\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:=\int\:\:\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}} \frac{\mathrm{4}}{\mathrm{3}}\:\:\:\int\:\:\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+{c}_{\mathrm{2}} \:\Rightarrow \\ $$$${ln}\mid{y}\mid\:={ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)+\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+{c}\:\Rightarrow \\ $$$${y}\left({x}\right)\:={K}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\:{e}^{\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)} \:\:\:{let}\:{use}\:{mvc}\:{method} \\ $$$${y}^{'} \:={K}^{'} \left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\:{e}^{\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}\:}\:{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}\:}\right)\:} \:+{K}\left\{\:\left(\mathrm{2}{x}−\mathrm{1}\right){e}^{\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)} \right. \\ $$$$\left.+\left.\left({x}^{\mathrm{2}} −{x}\:+\mathrm{1}\right)×\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}\:\:\:\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}\left(\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \right)}\:\right\}\right\}{e}^{\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)} \\ $$$$=\left\{{K}^{'} \left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)+\left(\mathrm{2}{x}−\mathrm{1}\right){K}+\:\frac{\mathrm{16}}{\mathrm{3}}\:{K}\left({x}^{\mathrm{2}} −{x}\:+\mathrm{1}\right)×\frac{\mathrm{1}}{\mathrm{1}+\frac{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}}}\right\} \\ $$$$×{e}^{\frac{\mathrm{8}}{\:\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)} ….{be}\:{continued}…. \\ $$
