Menu Close

solve-the-differential-equation-2-d-2-y-dx-2-dy-dx-e-x-4-

Tinku Tara 0 Comments
Pin




Question Number 66420 by Rio Michael last updated on 14/Aug/19
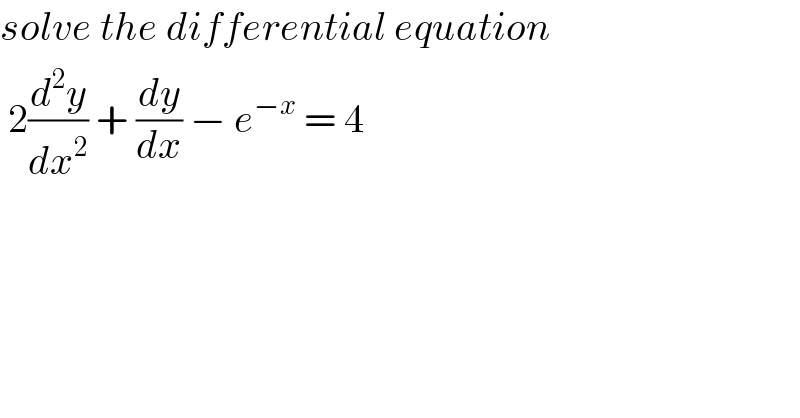
solve the differential equation 2(d^2 y/dx^2 ) + (dy/dx) − e^(−x) = 4
$${solve}\:{the}\:{differential}\:{equation} \\ $$$$\:\mathrm{2}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\frac{{dy}}{{dx}}\:−\:{e}^{−{x}} \:=\:\mathrm{4} \\ $$
Commented by mathmax by abdo last updated on 14/Aug/19
2y^(′′) +y^′ =4 +e^(−x) let y^′ =z so (e) ⇒2z^′ +z =4+e^(−x) (e^′ ) (he) →2z^′ +z =0 ⇒2z^′ =−z ⇒(z^′ /z)=−(1/2) ⇒ln∣z∣=−(x/2) +λ ⇒ z(x)= K e^(−(x/2)) let use mvc method z^′ =K^′ e^(−(x/2)) −(K/2)e^(−(x/2)) (e^′ )⇒2K^′ e^(−(x/2)) −K e^(−(x/2)) +K e^(−(x/2)) =4+e^(−x) ⇒2K^′ e^(−(x/2)) =4+e^(−x ) ⇒ K^′ =(1/2) e^(x/2) (4+e^(−x) ) =2 e^(x/2) +(1/2) e^(−(x/2)) ⇒ K(x) =∫ (2e^(x/2) +(1/2)e^(−(x/2)) )dx+c =4 e^(x/2) −e^(−(x/2)) +c ⇒ z(x) =e^(−(x/2)) {4e^(x/2) −e^(−(x/2)) +c} =4 −e^(−x) +c e^(−(x/2)) y^′ =z ⇒ y^(′ ) =4−e^(−x) +c e^(−(x/2)) ⇒y(x) =∫ (4−e^(−x) +c e^(−(x/2)) )dx +λ ⇒ y(x)=4x +e^(−x) −2c e^(−(x/2)) +λ
$$\mathrm{2}{y}^{''} +{y}^{'} \:=\mathrm{4}\:+{e}^{−{x}} \:\:\:{let}\:{y}^{'} \:={z}\:\:{so}\:\left({e}\right)\:\Rightarrow\mathrm{2}{z}^{'} \:+{z}\:=\mathrm{4}+{e}^{−{x}} \:\:\:\left({e}^{'} \right) \\ $$$$\left({he}\right)\:\rightarrow\mathrm{2}{z}^{'} \:+{z}\:=\mathrm{0}\:\Rightarrow\mathrm{2}{z}^{'} \:=−{z}\:\Rightarrow\frac{{z}^{'} }{{z}}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{ln}\mid{z}\mid=−\frac{{x}}{\mathrm{2}}\:+\lambda\:\Rightarrow \\ $$$${z}\left({x}\right)=\:{K}\:{e}^{−\frac{{x}}{\mathrm{2}}} \:\:\:\:{let}\:{use}\:{mvc}\:{method}\: \\ $$$${z}^{'} \:={K}^{'} \:{e}^{−\frac{{x}}{\mathrm{2}}} \:−\frac{{K}}{\mathrm{2}}{e}^{−\frac{{x}}{\mathrm{2}}} \\ $$$$\left({e}^{'} \right)\Rightarrow\mathrm{2}{K}^{'} \:{e}^{−\frac{{x}}{\mathrm{2}}} \:−{K}\:{e}^{−\frac{{x}}{\mathrm{2}}} \:+{K}\:{e}^{−\frac{{x}}{\mathrm{2}}} \:=\mathrm{4}+{e}^{−{x}} \:\Rightarrow\mathrm{2}{K}^{'} \:{e}^{−\frac{{x}}{\mathrm{2}}} \:=\mathrm{4}+{e}^{−{x}\:} \Rightarrow \\ $$$${K}^{'} \:=\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{\frac{{x}}{\mathrm{2}}} \left(\mathrm{4}+{e}^{−{x}} \right)\:=\mathrm{2}\:{e}^{\frac{{x}}{\mathrm{2}}} \:+\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{−\frac{{x}}{\mathrm{2}}} \:\:\Rightarrow \\ $$$${K}\left({x}\right)\:=\int\:\:\left(\mathrm{2}{e}^{\frac{{x}}{\mathrm{2}}} \:+\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\frac{{x}}{\mathrm{2}}} \right){dx}+{c}\:=\mathrm{4}\:{e}^{\frac{{x}}{\mathrm{2}}} \:\:−{e}^{−\frac{{x}}{\mathrm{2}}} \:\:+{c}\:\Rightarrow \\ $$$${z}\left({x}\right)\:={e}^{−\frac{{x}}{\mathrm{2}}} \left\{\mathrm{4}{e}^{\frac{{x}}{\mathrm{2}}} \:−{e}^{−\frac{{x}}{\mathrm{2}}} \:+{c}\right\}\:=\mathrm{4}\:−{e}^{−{x}} \:+{c}\:{e}^{−\frac{{x}}{\mathrm{2}}} \\ $$$${y}^{'} \:={z}\:\Rightarrow\:{y}^{'\:} =\mathrm{4}−{e}^{−{x}} \:+{c}\:{e}^{−\frac{{x}}{\mathrm{2}}} \:\Rightarrow{y}\left({x}\right)\:=\int\:\left(\mathrm{4}−{e}^{−{x}} \:+{c}\:{e}^{−\frac{{x}}{\mathrm{2}}} \right){dx}\:+\lambda\:\Rightarrow \\ $$$${y}\left({x}\right)=\mathrm{4}{x}\:+{e}^{−{x}} \:−\mathrm{2}{c}\:{e}^{−\frac{{x}}{\mathrm{2}}} \:+\lambda \\ $$$$ \\ $$
Commented by Rio Michael last updated on 15/Aug/19
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 17/Aug/19
you are welcome.
$${you}\:{are}\:{welcome}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *