Question Number 8311 by lepan last updated on 07/Oct/16

$${Solve}\:{the}\:{equation}\:\mathrm{6}{cos}\mathrm{2}{a}−\mathrm{5}{sin}\mathrm{2}{a}=\mathrm{1}.\mathrm{8} \\ $$$${for}\mathrm{0}°\leqslant{a}\leqslant\mathrm{180}°. \\ $$
Commented by 123456 last updated on 07/Oct/16
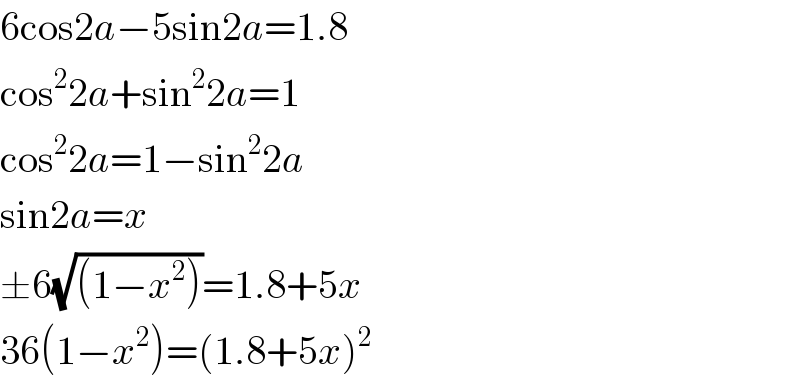
$$\mathrm{6cos2}{a}−\mathrm{5sin2}{a}=\mathrm{1}.\mathrm{8} \\ $$$$\mathrm{cos}^{\mathrm{2}} \mathrm{2}{a}+\mathrm{sin}^{\mathrm{2}} \mathrm{2}{a}=\mathrm{1} \\ $$$$\mathrm{cos}^{\mathrm{2}} \mathrm{2}{a}=\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{2}{a} \\ $$$$\mathrm{sin2}{a}={x} \\ $$$$\pm\mathrm{6}\sqrt{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}=\mathrm{1}.\mathrm{8}+\mathrm{5}{x} \\ $$$$\mathrm{36}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\left(\mathrm{1}.\mathrm{8}+\mathrm{5}{x}\right)^{\mathrm{2}} \\ $$
Answered by prakash jain last updated on 08/Oct/16
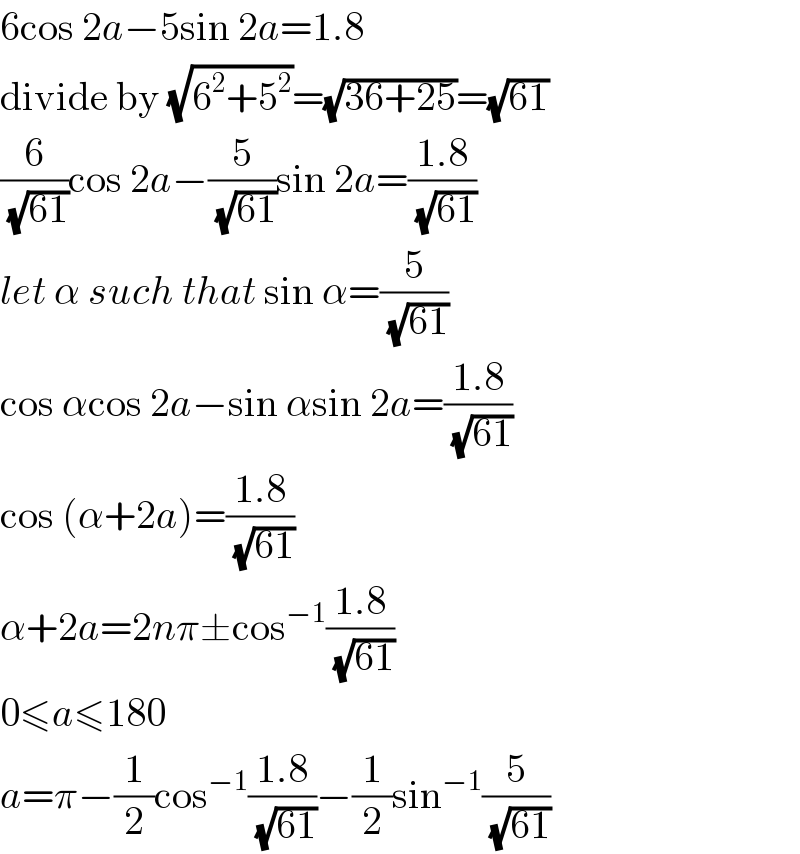
$$\mathrm{6cos}\:\mathrm{2}{a}−\mathrm{5sin}\:\mathrm{2}{a}=\mathrm{1}.\mathrm{8} \\ $$$$\mathrm{divide}\:\mathrm{by}\:\sqrt{\mathrm{6}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }=\sqrt{\mathrm{36}+\mathrm{25}}=\sqrt{\mathrm{61}} \\ $$$$\frac{\mathrm{6}}{\:\sqrt{\mathrm{61}}}\mathrm{cos}\:\mathrm{2}{a}−\frac{\mathrm{5}}{\:\sqrt{\mathrm{61}}}\mathrm{sin}\:\mathrm{2}{a}=\frac{\mathrm{1}.\mathrm{8}}{\:\sqrt{\mathrm{61}}} \\ $$$${let}\:\alpha\:{such}\:{that}\:\mathrm{sin}\:\alpha=\frac{\mathrm{5}}{\:\sqrt{\mathrm{61}}} \\ $$$$\mathrm{cos}\:\alpha\mathrm{cos}\:\mathrm{2}{a}−\mathrm{sin}\:\alpha\mathrm{sin}\:\mathrm{2}{a}=\frac{\mathrm{1}.\mathrm{8}}{\:\sqrt{\mathrm{61}}} \\ $$$$\mathrm{cos}\:\left(\alpha+\mathrm{2}{a}\right)=\frac{\mathrm{1}.\mathrm{8}}{\:\sqrt{\mathrm{61}}} \\ $$$$\alpha+\mathrm{2}{a}=\mathrm{2}{n}\pi\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}.\mathrm{8}}{\:\sqrt{\mathrm{61}}} \\ $$$$\mathrm{0}\leqslant{a}\leqslant\mathrm{180} \\ $$$${a}=\pi−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}.\mathrm{8}}{\:\sqrt{\mathrm{61}}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{5}}{\:\sqrt{\mathrm{61}}} \\ $$
