Question Number 12532 by tawa last updated on 24/Apr/17
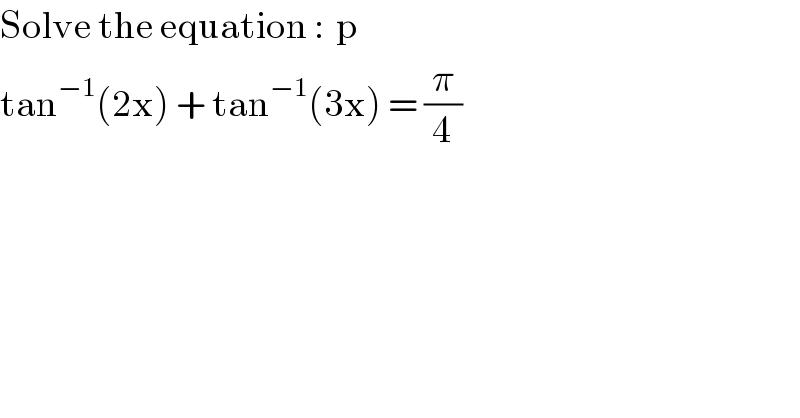
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}\::\:\:\mathrm{p} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2x}\right)\:+\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3x}\right)\:=\:\frac{\pi}{\mathrm{4}} \\ $$
Answered by mrW1 last updated on 25/Apr/17
![tan [tan^(−1) (2x) + tan^(−1) (3x)] = tan ((π/4)) ((2x+3x)/(1−2x×3x))=1 5x=1−6x^2 6x^2 +5x−1=0 (6x−1)(x+1)=0 x=(1/6) x=−1 (no solution, since x>0)](https://www.tinkutara.com/question/Q12536.png)
$$\mathrm{tan}\:\left[\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2x}\right)\:+\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3x}\right)\right]\:=\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}\right) \\ $$$$\frac{\mathrm{2}{x}+\mathrm{3}{x}}{\mathrm{1}−\mathrm{2}{x}×\mathrm{3}{x}}=\mathrm{1} \\ $$$$\mathrm{5}{x}=\mathrm{1}−\mathrm{6}{x}^{\mathrm{2}} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{6}{x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${x}=−\mathrm{1}\:\left({no}\:{solution},\:{since}\:{x}>\mathrm{0}\right) \\ $$
Commented by tawa last updated on 25/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
