Menu Close

Solve-the-equation-x-4-2x-3-5x-2-10x-3-0-

Tinku Tara 0 Comments
Pin




Question Number 141672 by iloveisrael last updated on 22/May/21
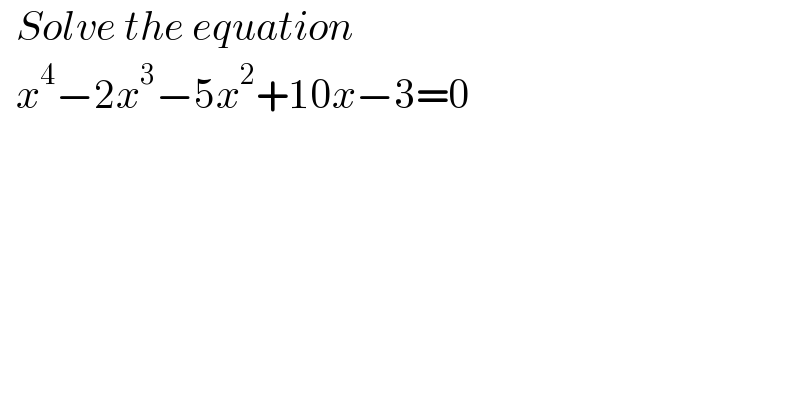
Solve the equation x^4 −2x^3 −5x^2 +10x−3=0
$$\:\:{Solve}\:{the}\:{equation}\: \\ $$$$\:\:{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{10}{x}−\mathrm{3}=\mathrm{0} \\ $$
Answered by MJS_new last updated on 22/May/21
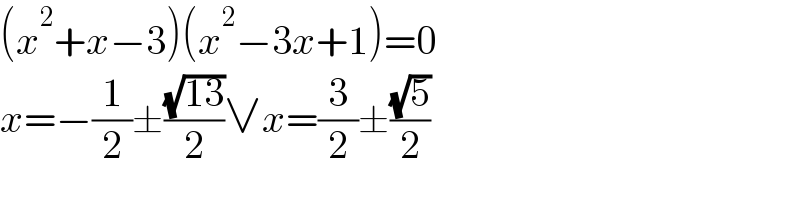
(x^2 +x−3)(x^2 −3x+1)=0 x=−(1/2)±((√(13))/2)∨x=(3/2)±((√5)/2)
$$\left({x}^{\mathrm{2}} +{x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}\vee{x}=\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 22/May/21
x^4 −2x^3 −5x^2 +10x−3=0 let x=t+(1/2) t^4 −((13)/2)t^2 +4t+(9/(16))=0 (t^2 −at−b)(t^2 +at−c)=0 t^4 −(a^2 +b+c)t^2 +a(c−b)t+bc=0 now match the constants { ((a^2 +b+c−((13)/2)=0)),((a(c−b)−4=0)),((bc−(9/(16))=0)) :} { ((b=−((2a^3 −13a+8)/(4a)))),((c=−((2a^3 −13a−8)/(4a)))),((((a^6 −13a^4 +40a^2 −16)/(4a^2 ))=0)) :} a^6 −13a^4 +40a^2 −16=0 select a “nice” solution of this a=2 ⇒ b=(1/4)∧c=(9/4) no insert backwards and it′s finished
$${x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{10}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{let}\:{x}={t}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${t}^{\mathrm{4}} −\frac{\mathrm{13}}{\mathrm{2}}{t}^{\mathrm{2}} +\mathrm{4}{t}+\frac{\mathrm{9}}{\mathrm{16}}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} −{at}−{b}\right)\left({t}^{\mathrm{2}} +{at}−{c}\right)=\mathrm{0} \\ $$$${t}^{\mathrm{4}} −\left({a}^{\mathrm{2}} +{b}+{c}\right){t}^{\mathrm{2}} +{a}\left({c}−{b}\right){t}+{bc}=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{match}\:\mathrm{the}\:\mathrm{constants} \\ $$$$\begin{cases}{{a}^{\mathrm{2}} +{b}+{c}−\frac{\mathrm{13}}{\mathrm{2}}=\mathrm{0}}\\{{a}\left({c}−{b}\right)−\mathrm{4}=\mathrm{0}}\\{{bc}−\frac{\mathrm{9}}{\mathrm{16}}=\mathrm{0}}\end{cases} \\ $$$$\begin{cases}{{b}=−\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{13}{a}+\mathrm{8}}{\mathrm{4}{a}}}\\{{c}=−\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{13}{a}−\mathrm{8}}{\mathrm{4}{a}}}\\{\frac{{a}^{\mathrm{6}} −\mathrm{13}{a}^{\mathrm{4}} +\mathrm{40}{a}^{\mathrm{2}} −\mathrm{16}}{\mathrm{4}{a}^{\mathrm{2}} }=\mathrm{0}}\end{cases} \\ $$$${a}^{\mathrm{6}} −\mathrm{13}{a}^{\mathrm{4}} +\mathrm{40}{a}^{\mathrm{2}} −\mathrm{16}=\mathrm{0} \\ $$$$\mathrm{select}\:\mathrm{a}\:“\mathrm{nice}''\:\mathrm{solution}\:\mathrm{of}\:\mathrm{this} \\ $$$${a}=\mathrm{2} \\ $$$$\Rightarrow\:{b}=\frac{\mathrm{1}}{\mathrm{4}}\wedge{c}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{no}\:\mathrm{insert}\:\mathrm{backwards}\:\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{finished} \\ $$
Commented by iloveisrael last updated on 22/May/21
yes. it same by Ferrari′s method
$${yes}.\:{it}\:{same}\:{by}\:{Ferrari}'{s}\:{method} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *