Question Number 66756 by John Kaloki Musau last updated on 19/Aug/19
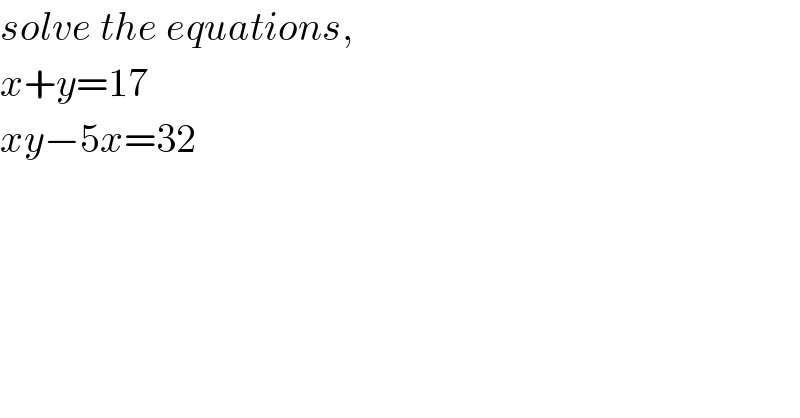
$${solve}\:{the}\:{equations}, \\ $$$${x}+{y}=\mathrm{17} \\ $$$${xy}−\mathrm{5}{x}=\mathrm{32} \\ $$
Answered by $@ty@m123 last updated on 19/Aug/19
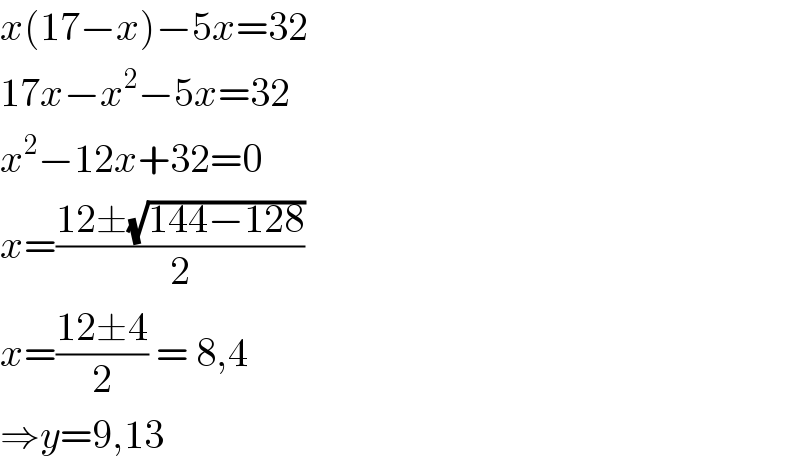
$${x}\left(\mathrm{17}−{x}\right)−\mathrm{5}{x}=\mathrm{32} \\ $$$$\mathrm{17}{x}−{x}^{\mathrm{2}} −\mathrm{5}{x}=\mathrm{32} \\ $$$${x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{32}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{12}\pm\sqrt{\mathrm{144}−\mathrm{128}}}{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{12}\pm\mathrm{4}}{\mathrm{2}}\:=\:\mathrm{8},\mathrm{4} \\ $$$$\Rightarrow{y}=\mathrm{9},\mathrm{13} \\ $$
Answered by John Kaloki Musau last updated on 20/Aug/19
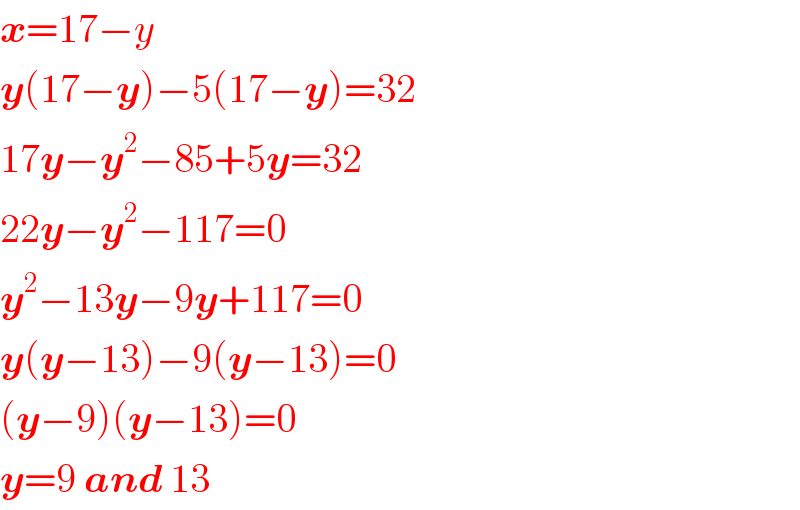
$$\boldsymbol{{x}}=\mathrm{17}−{y} \\ $$$$\boldsymbol{{y}}\left(\mathrm{17}−\boldsymbol{{y}}\right)−\mathrm{5}\left(\mathrm{17}−\boldsymbol{{y}}\right)=\mathrm{32} \\ $$$$\mathrm{17}\boldsymbol{{y}}−\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{85}+\mathrm{5}\boldsymbol{{y}}=\mathrm{32} \\ $$$$\mathrm{22}\boldsymbol{{y}}−\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{117}=\mathrm{0} \\ $$$$\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{13}\boldsymbol{{y}}−\mathrm{9}\boldsymbol{{y}}+\mathrm{117}=\mathrm{0} \\ $$$$\boldsymbol{{y}}\left(\boldsymbol{{y}}−\mathrm{13}\right)−\mathrm{9}\left(\boldsymbol{{y}}−\mathrm{13}\right)=\mathrm{0} \\ $$$$\left(\boldsymbol{{y}}−\mathrm{9}\right)\left(\boldsymbol{{y}}−\mathrm{13}\right)=\mathrm{0} \\ $$$$\boldsymbol{{y}}=\mathrm{9}\:\boldsymbol{{and}}\:\mathrm{13} \\ $$
