Solve-the-following-compound-inequation-in-interval-0-2pi-tan-x-2-1-and-tan-x-2-lt-0-

Question Number 1418 by Rasheed Ahmad last updated on 04/Aug/15

S o l v e t h e f o l l o w i n g c o m p o u n d

i n e q u a t i o n i n i n t e r v a l (0, 2 π),

t a n \frac{x}{2} ⩽ - 1 a n d t a n \frac{x}{2} < 0 .

Commented by 123456 last updated on 31/Jul/15

\tan \frac{π}{4} = - \tan \frac{3 π}{4} = \tan \frac{5 π}{4} = - \tan \frac{7 π}{4} = 1

Answered by 123456 last updated on 31/Jul/15

\tan \frac{x}{2} < 0

\frac{x}{2} \in (\frac{π}{2} + 2 π k, π + 2 π k) \cup (\frac{3 π}{2} + 2 π k, 2 π + 2 π k), k \in Z

x \in (π + 4 π k, 2 π + 4 π k) \cup (3 π + 4 π k, 4 π + 4 π k)

\tan \frac{x}{2} ⩽ - 1

\frac{x}{2} \in (\frac{π}{2} + 2 π k, \frac{3 π}{4} + 2 π k] \cup (\frac{3 π}{2} + 2 π k, \frac{7 π}{4} + 2 π k]

x \in (π + 4 π k, \frac{3 π}{2} + 4 π k] \cup (3 π + 4 π k, \frac{7 π}{2} + 4 π k]

Commented by Rasheed Ahmad last updated on 03/Aug/15

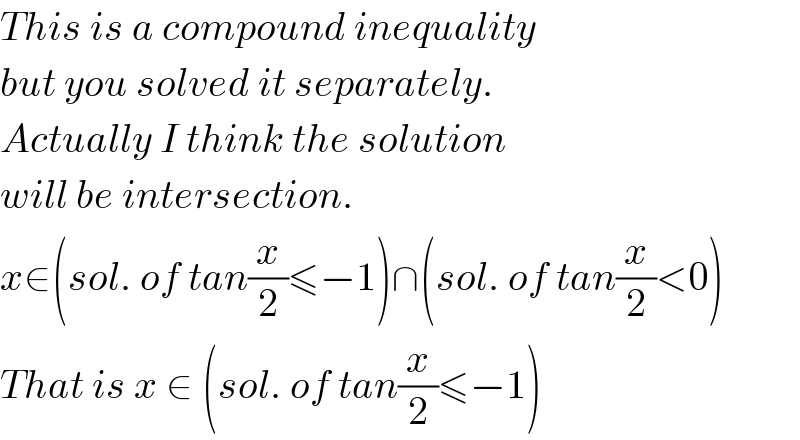
T h i s i s a c o m p o u n d i n e q u a l i t y

b u t y o u s o l v e d i t s e p a r a t e l y .

A c t u a l l y I t h i n k t h e s o l u t i o n

w i l l b e i n t e r s e c t i o n .

x \in (s o l . o f t a n \frac{x}{2} ⩽ - 1) \cap (s o l . o f t a n \frac{x}{2} < 0)

T h a t i s x \in (s o l . o f t a n \frac{x}{2} ⩽ - 1)

Commented by 123456 last updated on 03/Aug/15

yes, i {didn}^{'} t see it, the solution then

is the intersection of these two solution

x \in (π + 4 π k, \frac{3 π}{2} + 4 π k] \cup (3 π + 4 π k, \frac{7 π}{2} + 4 π k]

for x \in [0, 2 π) we have

x \in (π, \frac{3 π}{2}]

Facebook Tweet Pin