Question Number 823 by 112358 last updated on 18/Mar/15
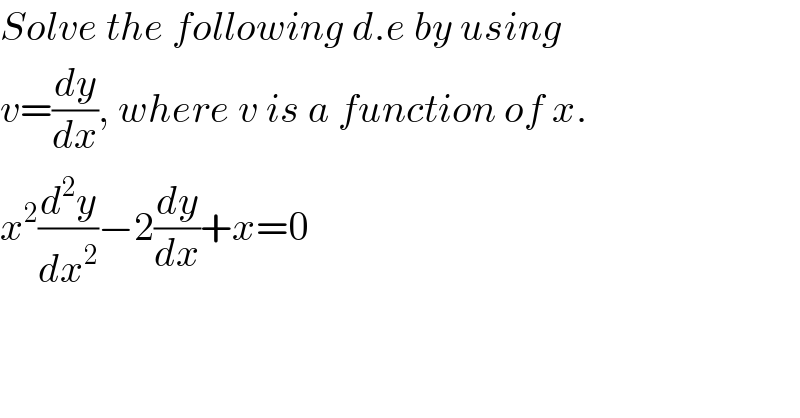
$${Solve}\:{the}\:{following}\:{d}.{e}\:{by}\:{using} \\ $$$${v}=\frac{{dy}}{{dx}},\:{where}\:{v}\:{is}\:{a}\:{function}\:{of}\:{x}. \\ $$$${x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }−\mathrm{2}\frac{{dy}}{{dx}}+{x}=\mathrm{0} \\ $$
Answered by 123456 last updated on 18/Mar/15
![v=(dy/dx)⇒(dv/dx)=(d^2 y/dx^2 ) x^2 (d^2 y/dx^2 )−2(dy/dx)+x=0⇒x^2 (dv/dx)−2v+x=0 by the coment v=−e^(−(2/x)) ∫(e^(2/x) /x)dx (dy/dx)=−e^(−(2/x)) ∫(e^(2/x) /x)dx y=∫−e^(−(2/x)) ∫(e^(2/x) /x)dxdx y=−∫e^(−(2/x)) ∫(e^(2/x) /x)dxdx Ei(u)=∫(e^u /u)du ∫(e^(2/x) /x)dx u=(2/x)⇔x=(2/u) du=−((2dx)/x^2 )⇔−((xdu)/2)=(dx/x)⇔−(du/u)=(dx/x) −∫(e^u /u)du=−Ei(u)+C_1 =−Ei((2/x))+C_1 y=∫−e^(−(2/x)) [−Ei((2/x))+C_1 ]dx y=∫e^(−(2/x)) Ei((2/x))dx−C_1 ∫e^(−(2/x)) dx](https://www.tinkutara.com/question/Q824.png)
$${v}=\frac{{dy}}{{dx}}\Rightarrow\frac{{dv}}{{dx}}=\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }−\mathrm{2}\frac{{dy}}{{dx}}+{x}=\mathrm{0}\Rightarrow{x}^{\mathrm{2}} \frac{{dv}}{{dx}}−\mathrm{2}{v}+{x}=\mathrm{0} \\ $$$${by}\:{the}\:{coment} \\ $$$${v}=−{e}^{−\frac{\mathrm{2}}{{x}}} \int\frac{{e}^{\frac{\mathrm{2}}{{x}}} }{{x}}{dx} \\ $$$$\frac{{dy}}{{dx}}=−{e}^{−\frac{\mathrm{2}}{{x}}} \int\frac{{e}^{\frac{\mathrm{2}}{{x}}} }{{x}}{dx} \\ $$$${y}=\int−{e}^{−\frac{\mathrm{2}}{{x}}} \int\frac{{e}^{\frac{\mathrm{2}}{{x}}} }{{x}}{dxdx} \\ $$$${y}=−\int{e}^{−\frac{\mathrm{2}}{{x}}} \int\frac{{e}^{\frac{\mathrm{2}}{{x}}} }{{x}}{dxdx} \\ $$$$\mathrm{E}{i}\left({u}\right)=\int\frac{{e}^{{u}} }{{u}}{du} \\ $$$$\int\frac{{e}^{\frac{\mathrm{2}}{{x}}} }{{x}}{dx} \\ $$$${u}=\frac{\mathrm{2}}{{x}}\Leftrightarrow{x}=\frac{\mathrm{2}}{{u}} \\ $$$${du}=−\frac{\mathrm{2}{dx}}{{x}^{\mathrm{2}} }\Leftrightarrow−\frac{{xdu}}{\mathrm{2}}=\frac{{dx}}{{x}}\Leftrightarrow−\frac{{du}}{{u}}=\frac{{dx}}{{x}} \\ $$$$−\int\frac{{e}^{{u}} }{{u}}{du}=−\mathrm{Ei}\left(\mathrm{u}\right)+\mathrm{C}_{\mathrm{1}} =−\mathrm{Ei}\left(\frac{\mathrm{2}}{{x}}\right)+\mathrm{C}_{\mathrm{1}} \\ $$$${y}=\int−{e}^{−\frac{\mathrm{2}}{{x}}} \left[−\mathrm{Ei}\left(\frac{\mathrm{2}}{{x}}\right)+\mathrm{C}_{\mathrm{1}} \right]{dx} \\ $$$${y}=\int{e}^{−\frac{\mathrm{2}}{{x}}} \mathrm{Ei}\left(\frac{\mathrm{2}}{{x}}\right){dx}−\mathrm{C}_{\mathrm{1}} \int{e}^{−\frac{\mathrm{2}}{{x}}} {dx} \\ $$
Commented by 123456 last updated on 18/Mar/15
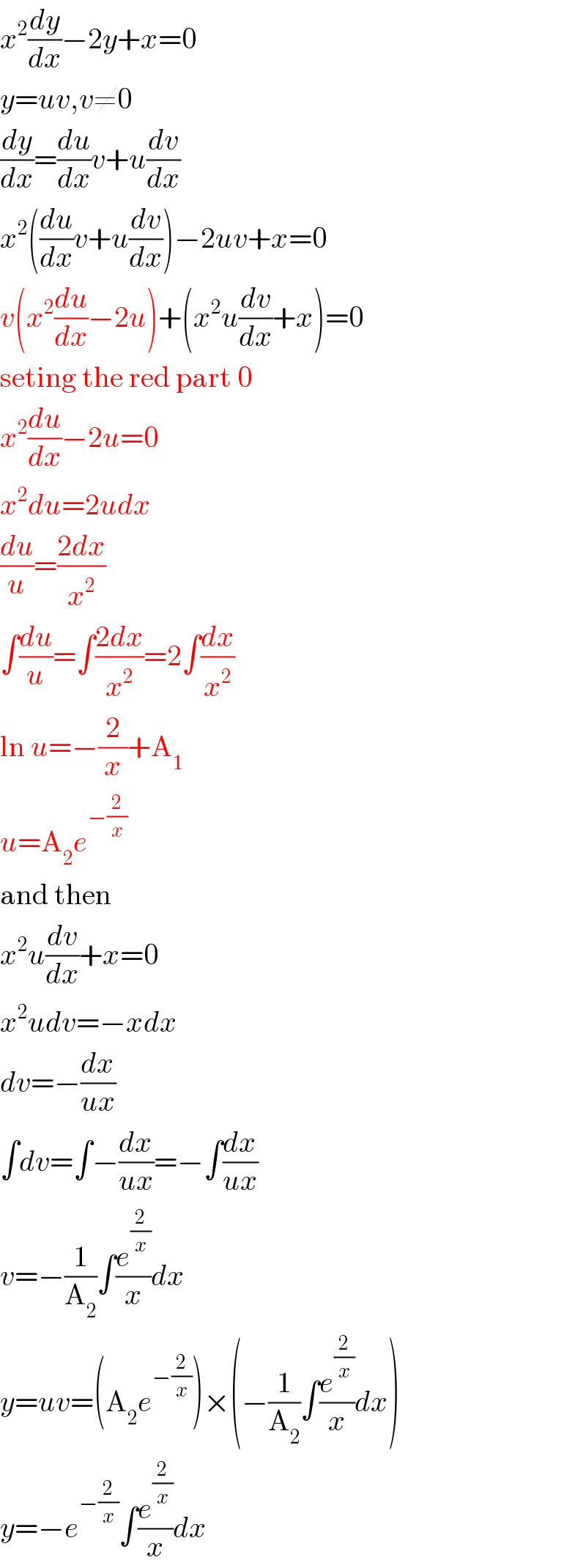
$${x}^{\mathrm{2}} \frac{{dy}}{{dx}}−\mathrm{2}{y}+{x}=\mathrm{0} \\ $$$${y}={uv},{v}\neq\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=\frac{{du}}{{dx}}{v}+{u}\frac{{dv}}{{dx}} \\ $$$${x}^{\mathrm{2}} \left(\frac{{du}}{{dx}}{v}+{u}\frac{{dv}}{{dx}}\right)−\mathrm{2}{uv}+{x}=\mathrm{0} \\ $$$${v}\left({x}^{\mathrm{2}} \frac{{du}}{{dx}}−\mathrm{2}{u}\right)+\left({x}^{\mathrm{2}} {u}\frac{{dv}}{{dx}}+{x}\right)=\mathrm{0} \\ $$$$\mathrm{seting}\:\mathrm{the}\:\mathrm{red}\:\mathrm{part}\:\mathrm{0} \\ $$$${x}^{\mathrm{2}} \frac{{du}}{{dx}}−\mathrm{2}{u}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} {du}=\mathrm{2}{udx} \\ $$$$\frac{{du}}{{u}}=\frac{\mathrm{2}{dx}}{{x}^{\mathrm{2}} } \\ $$$$\int\frac{{du}}{{u}}=\int\frac{\mathrm{2}{dx}}{{x}^{\mathrm{2}} }=\mathrm{2}\int\frac{{dx}}{{x}^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:{u}=−\frac{\mathrm{2}}{{x}}+\mathrm{A}_{\mathrm{1}} \\ $$$${u}=\mathrm{A}_{\mathrm{2}} {e}^{−\frac{\mathrm{2}}{{x}}} \\ $$$$\mathrm{and}\:\mathrm{then} \\ $$$${x}^{\mathrm{2}} {u}\frac{{dv}}{{dx}}+{x}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} {udv}=−{xdx} \\ $$$${dv}=−\frac{{dx}}{{ux}} \\ $$$$\int{dv}=\int−\frac{{dx}}{{ux}}=−\int\frac{{dx}}{{ux}} \\ $$$${v}=−\frac{\mathrm{1}}{\mathrm{A}_{\mathrm{2}} }\int\frac{{e}^{\frac{\mathrm{2}}{{x}}} }{{x}}{dx} \\ $$$${y}={uv}=\left(\mathrm{A}_{\mathrm{2}} {e}^{−\frac{\mathrm{2}}{{x}}} \right)×\left(−\frac{\mathrm{1}}{\mathrm{A}_{\mathrm{2}} }\int\frac{{e}^{\frac{\mathrm{2}}{{x}}} }{{x}}{dx}\right) \\ $$$${y}=−{e}^{−\frac{\mathrm{2}}{{x}}} \int\frac{{e}^{\frac{\mathrm{2}}{{x}}} }{{x}}{dx} \\ $$
