Question Number 1575 by 112358 last updated on 21/Aug/15
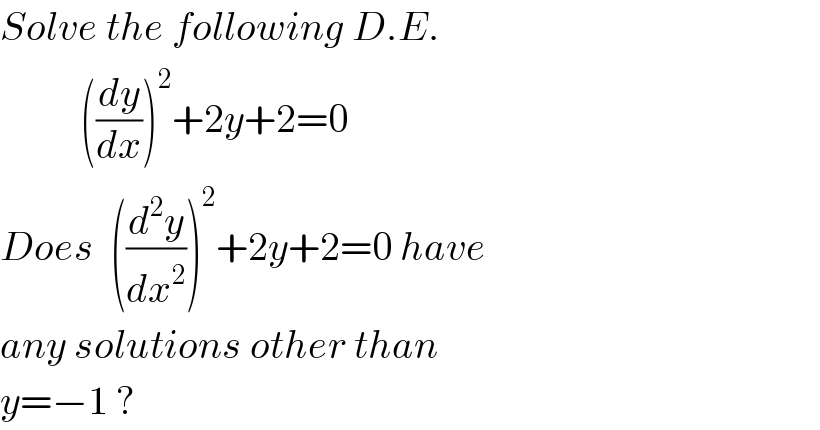
$${Solve}\:{the}\:{following}\:{D}.{E}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} +\mathrm{2}{y}+\mathrm{2}=\mathrm{0}\: \\ $$$${Does}\:\:\left(\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right)^{\mathrm{2}} +\mathrm{2}{y}+\mathrm{2}=\mathrm{0}\:{have} \\ $$$${any}\:{solutions}\:{other}\:{than} \\ $$$${y}=−\mathrm{1}\:? \\ $$
Commented by 123456 last updated on 21/Aug/15
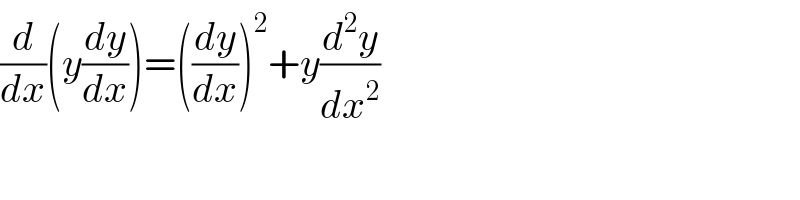
$$\frac{{d}}{{dx}}\left({y}\frac{{dy}}{{dx}}\right)=\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} +{y}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} } \\ $$
Answered by prakash jain last updated on 21/Aug/15

$${y}={c}_{\mathrm{1}} {x}^{\mathrm{2}} +{c}_{\mathrm{2}} {x}+{c}_{\mathrm{3}} \\ $$$${y}^{'} =\mathrm{2}{c}_{\mathrm{1}} {x}+{c}_{\mathrm{2}} \\ $$$$\left(\mathrm{2}{c}_{\mathrm{1}} {x}+{c}_{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{2}\left({c}_{\mathrm{1}} {x}^{\mathrm{2}} +{c}_{\mathrm{2}} {x}+{c}_{\mathrm{3}} \right)+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{4}{c}_{\mathrm{1}} ^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{4}{c}_{\mathrm{1}} {c}_{\mathrm{2}} {x}+{c}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{c}_{\mathrm{1}} {x}^{\mathrm{2}} +\mathrm{2}{c}_{\mathrm{2}} {x}+\mathrm{2}{c}_{\mathrm{3}} +\mathrm{2}=\mathrm{0} \\ $$$${c}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\:{or}\:{c}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{4}{c}_{\mathrm{1}} {c}_{\mathrm{2}} +\mathrm{2}{c}_{\mathrm{2}} =\mathrm{0} \\ $$$${c}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{c}_{\mathrm{3}} +\mathrm{2}=\mathrm{0}\Rightarrow{c}_{\mathrm{3}} =−\frac{{c}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1} \\ $$$${y}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{c}_{\mathrm{2}} {x}−\left(\frac{{c}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}}{\mathrm{2}}\right) \\ $$$$\mathrm{The}\:\mathrm{second}\:\mathrm{differential}\:\mathrm{equation}\:\mathrm{should}\:\mathrm{result} \\ $$$$\mathrm{in}\:\mathrm{a}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{with}\:\mathrm{2}\:\mathrm{arbitrary}\:\mathrm{constants}. \\ $$
