Menu Close

Solve-the-system-of-equation-x-2-yz-52-i-y-2-xz-6-ii-z-2-xy-86-iii-

Tinku Tara 0 Comments
Pin




Question Number 6105 by sanusihammed last updated on 13/Jun/16
Solve the system of equation x^2 − yz = − 52 .............. (i) y^2 − xz = − 6 ................ (ii) z^2 − xy = 86 .............. (iii)
$${Solve}\:{the}\:{system}\:{of}\:{equation}\: \\ $$$$ \\ $$$${x}^{\mathrm{2}} \:−\:{yz}\:=\:−\:\mathrm{52}\:\:\:…………..\:\left({i}\right) \\ $$$${y}^{\mathrm{2}} \:−\:{xz}\:=\:−\:\mathrm{6}\:…………….\:\left({ii}\right) \\ $$$${z}^{\mathrm{2}} \:−\:{xy}\:=\:\mathrm{86}\:\:\:…………..\:\left({iii}\right) \\ $$
Commented by Rasheed Soomro last updated on 14/Jun/16
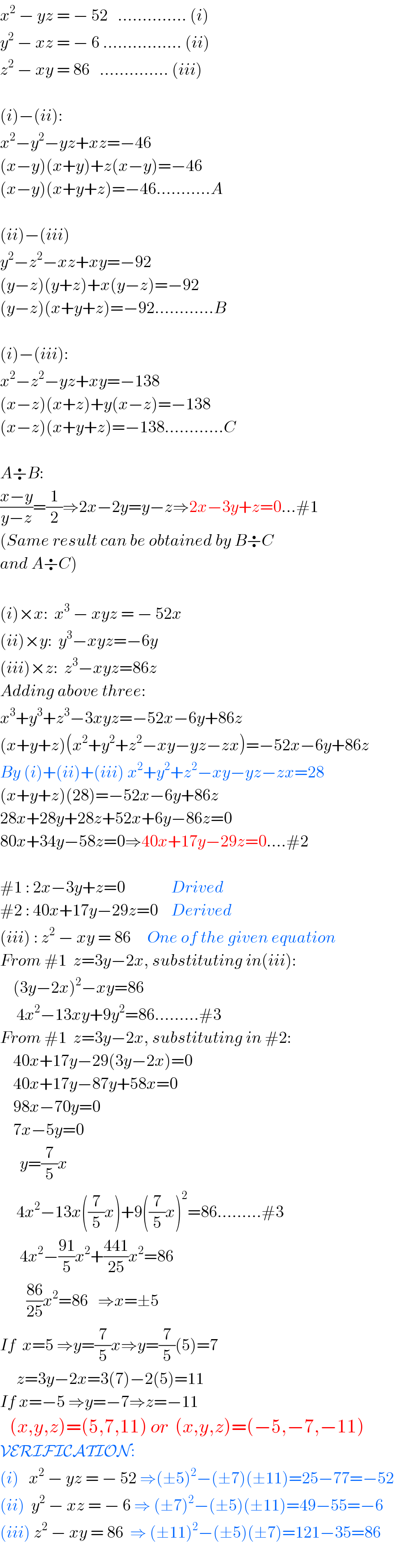
x^2 − yz = − 52 .............. (i) y^2 − xz = − 6 ................ (ii) z^2 − xy = 86 .............. (iii) (i)−(ii): x^2 −y^2 −yz+xz=−46 (x−y)(x+y)+z(x−y)=−46 (x−y)(x+y+z)=−46...........A (ii)−(iii) y^2 −z^2 −xz+xy=−92 (y−z)(y+z)+x(y−z)=−92 (y−z)(x+y+z)=−92............B (i)−(iii): x^2 −z^2 −yz+xy=−138 (x−z)(x+z)+y(x−z)=−138 (x−z)(x+y+z)=−138............C A÷B: ((x−y)/(y−z))=(1/2)⇒2x−2y=y−z⇒2x−3y+z=0...#1 (Same result can be obtained by B÷C and A÷C) (i)×x: x^3 − xyz = − 52x (ii)×y: y^3 −xyz=−6y (iii)×z: z^3 −xyz=86z Adding above three: x^3 +y^3 +z^3 −3xyz=−52x−6y+86z (x+y+z)(x^2 +y^2 +z^2 −xy−yz−zx)=−52x−6y+86z By (i)+(ii)+(iii) x^2 +y^2 +z^2 −xy−yz−zx=28 (x+y+z)(28)=−52x−6y+86z 28x+28y+28z+52x+6y−86z=0 80x+34y−58z=0⇒40x+17y−29z=0....#2 #1 : 2x−3y+z=0 Drived #2 : 40x+17y−29z=0 Derived (iii) : z^2 − xy = 86 One of the given equation From #1 z=3y−2x, substituting in(iii): (3y−2x)^2 −xy=86 4x^2 −13xy+9y^2 =86.........#3 From #1 z=3y−2x, substituting in #2: 40x+17y−29(3y−2x)=0 40x+17y−87y+58x=0 98x−70y=0 7x−5y=0 y=(7/5)x 4x^2 −13x((7/5)x)+9((7/5)x)^2 =86.........#3 4x^2 −((91)/5)x^2 +((441)/(25))x^2 =86 ((86)/(25))x^2 =86 ⇒x=±5 If x=5 ⇒y=(7/5)x⇒y=(7/5)(5)=7 z=3y−2x=3(7)−2(5)=11 If x=−5 ⇒y=−7⇒z=−11 (x,y,z)=(5,7,11) or (x,y,z)=(−5,−7,−11) VERIFICATION: (i) x^2 − yz = − 52 ⇒(±5)^2 −(±7)(±11)=25−77=−52 (ii) y^2 − xz = − 6 ⇒ (±7)^2 −(±5)(±11)=49−55=−6 (iii) z^2 − xy = 86 ⇒ (±11)^2 −(±5)(±7)=121−35=86
$${x}^{\mathrm{2}} \:−\:{yz}\:=\:−\:\mathrm{52}\:\:\:…………..\:\left({i}\right) \\ $$$${y}^{\mathrm{2}} \:−\:{xz}\:=\:−\:\mathrm{6}\:…………….\:\left({ii}\right) \\ $$$${z}^{\mathrm{2}} \:−\:{xy}\:=\:\mathrm{86}\:\:\:…………..\:\left({iii}\right) \\ $$$$ \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} −{yz}+{xz}=−\mathrm{46} \\ $$$$\left({x}−{y}\right)\left({x}+{y}\right)+{z}\left({x}−{y}\right)=−\mathrm{46} \\ $$$$\left({x}−{y}\right)\left({x}+{y}+{z}\right)=−\mathrm{46}………..{A} \\ $$$$ \\ $$$$\left({ii}\right)−\left({iii}\right) \\ $$$${y}^{\mathrm{2}} −{z}^{\mathrm{2}} −{xz}+{xy}=−\mathrm{92} \\ $$$$\left({y}−{z}\right)\left({y}+{z}\right)+{x}\left({y}−{z}\right)=−\mathrm{92} \\ $$$$\left({y}−{z}\right)\left({x}+{y}+{z}\right)=−\mathrm{92}…………{B} \\ $$$$ \\ $$$$\left({i}\right)−\left({iii}\right): \\ $$$${x}^{\mathrm{2}} −{z}^{\mathrm{2}} −{yz}+{xy}=−\mathrm{138} \\ $$$$\left({x}−{z}\right)\left({x}+{z}\right)+{y}\left({x}−{z}\right)=−\mathrm{138} \\ $$$$\left({x}−{z}\right)\left({x}+{y}+{z}\right)=−\mathrm{138}…………{C} \\ $$$$ \\ $$$${A}\boldsymbol{\div}{B}: \\ $$$$\frac{{x}−{y}}{{y}−{z}}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{2}{x}−\mathrm{2}{y}={y}−{z}\Rightarrow\mathrm{2}{x}−\mathrm{3}{y}+{z}=\mathrm{0}…#\mathrm{1} \\ $$$$\left({Same}\:{result}\:{can}\:{be}\:{obtained}\:{by}\:{B}\boldsymbol{\div}{C}\:\right. \\ $$$$\left.{and}\:{A}\boldsymbol{\div}{C}\right) \\ $$$$\: \\ $$$$\left({i}\right)×{x}:\:\:{x}^{\mathrm{3}} \:−\:{xyz}\:=\:−\:\mathrm{52}{x} \\ $$$$\left({ii}\right)×{y}:\:\:{y}^{\mathrm{3}} −{xyz}=−\mathrm{6}{y} \\ $$$$\left({iii}\right)×{z}:\:\:{z}^{\mathrm{3}} −{xyz}=\mathrm{86}{z} \\ $$$${Adding}\:{above}\:{three}: \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mathrm{3}{xyz}=−\mathrm{52}{x}−\mathrm{6}{y}+\mathrm{86}{z} \\ $$$$\left({x}+{y}+{z}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{xy}−{yz}−{zx}\right)=−\mathrm{52}{x}−\mathrm{6}{y}+\mathrm{86}{z} \\ $$$${By}\:\left({i}\right)+\left({ii}\right)+\left({iii}\right)\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{xy}−{yz}−{zx}=\mathrm{28} \\ $$$$\left({x}+{y}+{z}\right)\left(\mathrm{28}\right)=−\mathrm{52}{x}−\mathrm{6}{y}+\mathrm{86}{z} \\ $$$$\mathrm{28}{x}+\mathrm{28}{y}+\mathrm{28}{z}+\mathrm{52}{x}+\mathrm{6}{y}−\mathrm{86}{z}=\mathrm{0} \\ $$$$\mathrm{80}{x}+\mathrm{34}{y}−\mathrm{58}{z}=\mathrm{0}\Rightarrow\mathrm{40}{x}+\mathrm{17}{y}−\mathrm{29}{z}=\mathrm{0}….#\mathrm{2} \\ $$$$ \\ $$$$#\mathrm{1}\::\:\mathrm{2}{x}−\mathrm{3}{y}+{z}=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Drived} \\ $$$$#\mathrm{2}\::\:\mathrm{40}{x}+\mathrm{17}{y}−\mathrm{29}{z}=\mathrm{0}\:\:\:\:{Derived} \\ $$$$\left({iii}\right)\::\:{z}^{\mathrm{2}} \:−\:{xy}\:=\:\mathrm{86}\:\:\:\:\:{One}\:{of}\:{the}\:{given}\:{equation} \\ $$$${From}\:#\mathrm{1}\:\:{z}=\mathrm{3}{y}−\mathrm{2}{x},\:{substituting}\:{in}\left({iii}\right): \\ $$$$\:\:\:\:\left(\mathrm{3}{y}−\mathrm{2}{x}\right)^{\mathrm{2}} −{xy}=\mathrm{86} \\ $$$$\:\:\:\:\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{13}{xy}+\mathrm{9}{y}^{\mathrm{2}} =\mathrm{86}………#\mathrm{3} \\ $$$${From}\:#\mathrm{1}\:\:{z}=\mathrm{3}{y}−\mathrm{2}{x},\:{substituting}\:{in}\:#\mathrm{2}: \\ $$$$\:\:\:\:\mathrm{40}{x}+\mathrm{17}{y}−\mathrm{29}\left(\mathrm{3}{y}−\mathrm{2}{x}\right)=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{40}{x}+\mathrm{17}{y}−\mathrm{87}{y}+\mathrm{58}{x}=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{98}{x}−\mathrm{70}{y}=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{7}{x}−\mathrm{5}{y}=\mathrm{0} \\ $$$$\:\:\:\:\:\:{y}=\frac{\mathrm{7}}{\mathrm{5}}{x} \\ $$$$\:\:\:\:\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{13}{x}\left(\frac{\mathrm{7}}{\mathrm{5}}{x}\right)+\mathrm{9}\left(\frac{\mathrm{7}}{\mathrm{5}}{x}\right)^{\mathrm{2}} =\mathrm{86}………#\mathrm{3} \\ $$$$\:\:\:\:\:\:\mathrm{4}{x}^{\mathrm{2}} −\frac{\mathrm{91}}{\mathrm{5}}{x}^{\mathrm{2}} +\frac{\mathrm{441}}{\mathrm{25}}{x}^{\mathrm{2}} =\mathrm{86} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{86}}{\mathrm{25}}{x}^{\mathrm{2}} =\mathrm{86}\:\:\:\Rightarrow{x}=\pm\mathrm{5} \\ $$$${If}\:\:{x}=\mathrm{5}\:\Rightarrow{y}=\frac{\mathrm{7}}{\mathrm{5}}{x}\Rightarrow{y}=\frac{\mathrm{7}}{\mathrm{5}}\left(\mathrm{5}\right)=\mathrm{7} \\ $$$$\:\:\:\:\:{z}=\mathrm{3}{y}−\mathrm{2}{x}=\mathrm{3}\left(\mathrm{7}\right)−\mathrm{2}\left(\mathrm{5}\right)=\mathrm{11} \\ $$$${If}\:{x}=−\mathrm{5}\:\Rightarrow{y}=−\mathrm{7}\Rightarrow{z}=−\mathrm{11} \\ $$$$\:\:\:\left({x},{y},{z}\right)=\left(\mathrm{5},\mathrm{7},\mathrm{11}\right)\:{or}\:\:\left({x},{y},{z}\right)=\left(−\mathrm{5},−\mathrm{7},−\mathrm{11}\right) \\ $$$$\mathcal{VERIFICATION}: \\ $$$$\left({i}\right)\:\:\:{x}^{\mathrm{2}} \:−\:{yz}\:=\:−\:\mathrm{52}\:\Rightarrow\left(\pm\mathrm{5}\right)^{\mathrm{2}} −\left(\pm\mathrm{7}\right)\left(\pm\mathrm{11}\right)=\mathrm{25}−\mathrm{77}=−\mathrm{52} \\ $$$$\left({ii}\right)\:\:{y}^{\mathrm{2}} \:−\:{xz}\:=\:−\:\mathrm{6}\:\Rightarrow\:\left(\pm\mathrm{7}\right)^{\mathrm{2}} −\left(\pm\mathrm{5}\right)\left(\pm\mathrm{11}\right)=\mathrm{49}−\mathrm{55}=−\mathrm{6} \\ $$$$\left({iii}\right)\:{z}^{\mathrm{2}} \:−\:{xy}\:=\:\mathrm{86}\:\:\Rightarrow\:\left(\pm\mathrm{11}\right)^{\mathrm{2}} −\left(\pm\mathrm{5}\right)\left(\pm\mathrm{7}\right)=\mathrm{121}−\mathrm{35}=\mathrm{86}\: \\ $$$$ \\ $$
Commented by Yozzii last updated on 14/Jun/16
nice
$${nice} \\ $$
Commented by sanusihammed last updated on 14/Jun/16
Wow thanks.
$${Wow}\:{thanks}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *