Menu Close

Solve-the-system-of-following-equation-xy-z-3-yz-x-18-zx-y-6-

Tinku Tara 0 Comments
Pin




Question Number 6275 by Rasheed Soomro last updated on 21/Jun/16
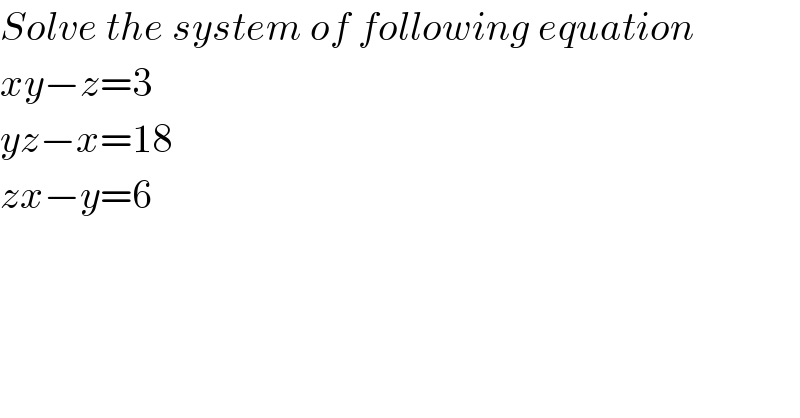
Solve the system of following equation xy−z=3 yz−x=18 zx−y=6
$${Solve}\:{the}\:{system}\:{of}\:{following}\:{equation} \\ $$$${xy}−{z}=\mathrm{3} \\ $$$${yz}−{x}=\mathrm{18} \\ $$$${zx}−{y}=\mathrm{6} \\ $$
Commented by sanusihammed last updated on 21/Jun/16
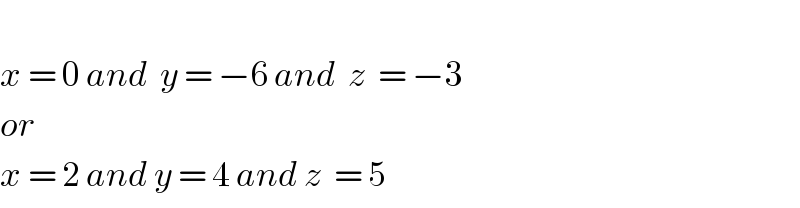
x = 0 and y = −6 and z = −3 or x = 2 and y = 4 and z = 5
$$ \\ $$$${x}\:=\:\mathrm{0}\:{and}\:\:{y}\:=\:−\mathrm{6}\:{and}\:\:{z}\:\:=\:−\mathrm{3} \\ $$$${or} \\ $$$${x}\:=\:\mathrm{2}\:{and}\:{y}\:=\:\mathrm{4}\:{and}\:{z}\:\:=\:\mathrm{5} \\ $$
Commented by Rasheed Soomro last updated on 21/Jun/16
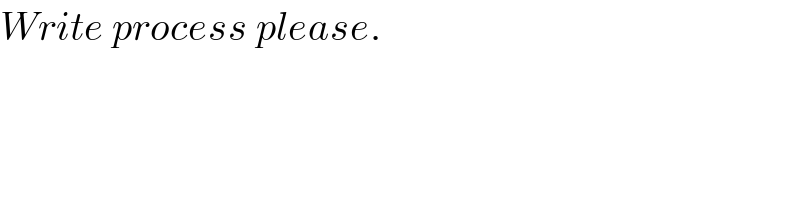
Write process please.
$${Write}\:{process}\:{please}. \\ $$
Commented by sanusihammed last updated on 21/Jun/16
Given xy − z = 3 ............ (i) yz − x = 18 ........ (ii) zx − y = 6 .......... (iii) Solving the first equation for z yields xy − z = 3 z = xy − 3 So the other two equation becomes yz − x = 18 y(xy − 3) − x = 18 xy^2 − 3y − x = 18 ............ (iv) And zx − y = 6 (xy − 3)x − y = 6 x^2 y − 3x − y = 6 ........... (v) Solving for y in (v) x^2 y − 3x − y = 6 y(x^2 − 1) − 3x = 6 y = ((3x + 6)/(x^2 − 1)) .......... (vi) Substitute this new value of y in (iv) xy^2 − 3y − x = 18 x(((3x + 6)/(x^2 − 1)))^2 − x − 3(((3x + 6)/(x^2 − 1))) = 18 Multiply through by (x^2 − 1)^2 x(3x + 6)^2 − x − 3(3x + 6)(x^2 − 1) = 18(x^2 − 1)^2 Simplify you will get x^5 + 18x^4 − 2x^(3 ) − 54x^2 − 44x = 0 x(x^4 + 18x^3 − 2x^2 − 54x − 44) = 0 x = 0 or x^4 + 18x^3 − 2x^2 − 54x − 44 = 0 Consider: x^4 + 18x^3 − 2x^2 − 54x − 44 = 0 By rational root theorem, we find that x = 2 is also a solution thus (x − 2) is a factor and we obtain (x − 2)(x^3 + 20x^2 + 38x + 22) = 0 x − 2 = 0 or x^3 + 20x^2 + 38x + 22 = 0 x = 2 and the other solution are irational. therefore, x = 0, x = 2 are the only real solution. from (iv) y = ((3x + 6)/(x^2 − 1)) when x = 0 y = ((3(0) + 6)/(0^2 − 1)) y = (6/(−1)) y = −6 when x = 0 and y = −6 then from z = xy − 3 z = 0(−6) − 3 z = −3 Thus, x = 0, y = −6, z = −3 Again for the second real number when x = 2 y = ((3(2) + 6)/((2)^2 − 1)) y = ((12)/3) y = 4 z = (2 × 4) − 3 z = 8 − 3 z = 5 Thus, x = 2, y = 4, z = 5 Those are the real answers. you can get other imaginary answers by solving the x^3 + 20x^2 + 38x + 22 DONE !
$${Given} \\ $$$${xy}\:−\:{z}\:=\:\mathrm{3}\:\:\:\:\:…………\:\left({i}\right) \\ $$$${yz}\:−\:{x}\:=\:\mathrm{18}\:\:\:\:……..\:\left({ii}\right) \\ $$$${zx}\:−\:{y}\:=\:\mathrm{6}\:\:\:\:\:\:……….\:\left({iii}\right) \\ $$$$ \\ $$$${Solving}\:{the}\:{first}\:{equation}\:{for}\:{z}\:{yields} \\ $$$${xy}\:−\:{z}\:=\:\mathrm{3} \\ $$$${z}\:=\:{xy}\:−\:\mathrm{3} \\ $$$$ \\ $$$${So}\:{the}\:{other}\:{two}\:{equation}\:{becomes} \\ $$$${yz}\:−\:{x}\:=\:\mathrm{18} \\ $$$${y}\left({xy}\:−\:\mathrm{3}\right)\:−\:{x}\:=\:\mathrm{18} \\ $$$${xy}^{\mathrm{2}} \:−\:\mathrm{3}{y}\:−\:{x}\:=\:\mathrm{18}\:\:\:\:…………\:\left({iv}\right) \\ $$$${And} \\ $$$${zx}\:−\:{y}\:=\:\mathrm{6} \\ $$$$\left({xy}\:−\:\mathrm{3}\right){x}\:−\:{y}\:=\:\mathrm{6} \\ $$$${x}^{\mathrm{2}} {y}\:−\:\mathrm{3}{x}\:−\:{y}\:=\:\mathrm{6}\:\:\:\:………..\:\left({v}\right) \\ $$$$ \\ $$$${Solving}\:{for}\:{y}\:{in}\:\left({v}\right) \\ $$$${x}^{\mathrm{2}} {y}\:−\:\mathrm{3}{x}\:−\:{y}\:=\:\mathrm{6} \\ $$$${y}\left({x}^{\mathrm{2}} \:−\:\mathrm{1}\right)\:−\:\mathrm{3}{x}\:=\:\mathrm{6} \\ $$$${y}\:=\:\frac{\mathrm{3}{x}\:+\:\mathrm{6}}{{x}^{\mathrm{2}} \:−\:\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……….\:\left({vi}\right) \\ $$$$ \\ $$$${Substitute}\:{this}\:{new}\:{value}\:{of}\:{y}\:{in}\:\left({iv}\right) \\ $$$${xy}^{\mathrm{2}} \:−\:\mathrm{3}{y}\:−\:{x}\:=\:\mathrm{18} \\ $$$${x}\left(\frac{\mathrm{3}{x}\:+\:\mathrm{6}}{{x}^{\mathrm{2}} \:−\:\mathrm{1}}\right)^{\mathrm{2}} −\:{x}\:−\:\mathrm{3}\left(\frac{\mathrm{3}{x}\:+\:\mathrm{6}}{{x}^{\mathrm{2}} \:−\:\mathrm{1}}\right)\:=\:\mathrm{18} \\ $$$$ \\ $$$${Multiply}\:{through}\:{by}\:\left({x}^{\mathrm{2}} \:−\:\mathrm{1}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${x}\left(\mathrm{3}{x}\:+\:\mathrm{6}\right)^{\mathrm{2}} \:−\:{x}\:−\:\mathrm{3}\left(\mathrm{3}{x}\:+\:\mathrm{6}\right)\left({x}^{\mathrm{2}} \:−\:\mathrm{1}\right)\:=\:\mathrm{18}\left({x}^{\mathrm{2}} \:−\:\mathrm{1}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${Simplify}\:{you}\:{will}\:{get}\: \\ $$$$ \\ $$$${x}^{\mathrm{5}} \:+\:\mathrm{18}{x}^{\mathrm{4}} \:−\:\mathrm{2}{x}^{\mathrm{3}\:} −\:\mathrm{54}{x}^{\mathrm{2}} \:−\:\mathrm{44}{x}\:=\:\mathrm{0} \\ $$$${x}\left({x}^{\mathrm{4}} \:+\:\mathrm{18}{x}^{\mathrm{3}} \:−\:\mathrm{2}{x}^{\mathrm{2}} \:−\:\mathrm{54}{x}\:−\:\mathrm{44}\right)\:=\:\mathrm{0} \\ $$$${x}\:=\:\mathrm{0}\:{or}\:{x}^{\mathrm{4}} \:+\:\mathrm{18}{x}^{\mathrm{3}} \:−\:\mathrm{2}{x}^{\mathrm{2}} \:−\:\mathrm{54}{x}\:−\:\mathrm{44}\:=\:\mathrm{0} \\ $$$$ \\ $$$${Consider}: \\ $$$${x}^{\mathrm{4}} \:+\:\mathrm{18}{x}^{\mathrm{3}} \:−\:\mathrm{2}{x}^{\mathrm{2}} \:−\:\mathrm{54}{x}\:−\:\mathrm{44}\:=\:\mathrm{0} \\ $$$$ \\ $$$${By}\:{rational}\:{root}\:{theorem},\:{we}\:{find}\:{that}\:{x}\:=\:\mathrm{2}\:{is}\:{also}\:{a}\: \\ $$$${solution} \\ $$$${thus}\:\left({x}\:−\:\mathrm{2}\right)\:{is}\:{a}\:{factor}\:{and}\:{we}\:{obtain} \\ $$$$ \\ $$$$\left({x}\:−\:\mathrm{2}\right)\left({x}^{\mathrm{3}} \:+\:\mathrm{20}{x}^{\mathrm{2}} \:+\:\mathrm{38}{x}\:+\:\mathrm{22}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$$${x}\:−\:\mathrm{2}\:=\:\mathrm{0}\:{or}\:{x}^{\mathrm{3}} \:+\:\mathrm{20}{x}^{\mathrm{2}} \:+\:\mathrm{38}{x}\:+\:\mathrm{22}\:=\:\mathrm{0} \\ $$$$ \\ $$$${x}\:=\:\mathrm{2}\:\:\:{and}\:{the}\:{other}\:{solution}\:{are}\:{irational}. \\ $$$$ \\ $$$${therefore},\: \\ $$$$ \\ $$$${x}\:=\:\mathrm{0},\:{x}\:=\:\mathrm{2}\:{are}\:{the}\:{only}\:{real}\:{solution}. \\ $$$$ \\ $$$${from}\:\left({iv}\right) \\ $$$$ \\ $$$${y}\:=\:\frac{\mathrm{3}{x}\:+\:\mathrm{6}}{{x}^{\mathrm{2}} \:−\:\mathrm{1}} \\ $$$${when}\:\:{x}\:\:=\:\:\mathrm{0} \\ $$$$ \\ $$$${y}\:=\:\frac{\mathrm{3}\left(\mathrm{0}\right)\:+\:\mathrm{6}}{\mathrm{0}^{\mathrm{2}} \:−\:\mathrm{1}}\:\: \\ $$$${y}\:=\:\frac{\mathrm{6}}{−\mathrm{1}} \\ $$$${y}\:=\:−\mathrm{6} \\ $$$$ \\ $$$${when}\:{x}\:=\:\mathrm{0}\:{and}\:{y}\:=\:−\mathrm{6} \\ $$$${then}\:{from} \\ $$$${z}\:=\:{xy}\:−\:\mathrm{3} \\ $$$${z}\:=\:\mathrm{0}\left(−\mathrm{6}\right)\:−\:\mathrm{3} \\ $$$${z}\:=\:−\mathrm{3} \\ $$$$ \\ $$$${Thus},\:{x}\:=\:\mathrm{0},\:{y}\:=\:−\mathrm{6},\:{z}\:=\:−\mathrm{3} \\ $$$$ \\ $$$${Again}\:{for}\:{the}\:{second}\:{real}\:{number} \\ $$$$ \\ $$$${when}\:{x}\:=\:\mathrm{2} \\ $$$${y}\:=\:\frac{\mathrm{3}\left(\mathrm{2}\right)\:+\:\mathrm{6}}{\left(\mathrm{2}\right)^{\mathrm{2}} \:−\:\mathrm{1}} \\ $$$${y}\:=\:\frac{\mathrm{12}}{\mathrm{3}} \\ $$$${y}\:=\:\mathrm{4} \\ $$$$ \\ $$$${z}\:=\:\left(\mathrm{2}\:×\:\mathrm{4}\right)\:−\:\mathrm{3} \\ $$$${z}\:=\:\mathrm{8}\:−\:\mathrm{3} \\ $$$${z}\:=\:\mathrm{5} \\ $$$$ \\ $$$${Thus},\:{x}\:=\:\mathrm{2},\:{y}\:=\:\mathrm{4},\:{z}\:=\:\mathrm{5} \\ $$$$ \\ $$$${Those}\:{are}\:{the}\:{real}\:{answers}.\:{you}\:{can}\:{get}\:{other}\:{imaginary}\: \\ $$$${answers}\:{by}\:{solving}\:{the}\:{x}^{\mathrm{3}} \:+\:\mathrm{20}{x}^{\mathrm{2}} \:+\:\mathrm{38}{x}\:+\:\mathrm{22} \\ $$$$ \\ $$$${DONE}\:! \\ $$
Commented by Rasheed Soomro last updated on 22/Jun/16
Good approach! I am also in search of a bit tricky method but have been not successful yet. I had solved Q#6105(suggested by you), which was somewhat resembling to this, in a tricky way.But this question is more challenging!
$$\mathrm{Good}\:\mathrm{approach}! \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{also}\:\mathrm{in}\:\mathrm{search}\:\mathrm{of}\:\:\mathrm{a}\:\mathrm{bit}\:\mathrm{tricky}\:\mathrm{method} \\ $$$$\mathrm{but}\:\mathrm{have}\:\mathrm{been}\:\mathrm{not}\:\mathrm{successful}\:\mathrm{yet}. \\ $$$${I}\:{had}\:{solved}\:{Q}#\mathrm{6105}\left({suggested}\:{by}\:{you}\right),\:{which}\:{was}\:{somewhat} \\ $$$${resembling}\:{to}\:{this},\:{in}\:{a}\:{tricky}\:{way}.{But}\:{this} \\ $$$${question}\:{is}\:{more}\:{challenging}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *