Menu Close

solve-the-value-of-x-logx-2-x-25-

Tinku Tara 0 Comments
Pin




Question Number 10248 by j.masanja06@gmail.com last updated on 31/Jan/17
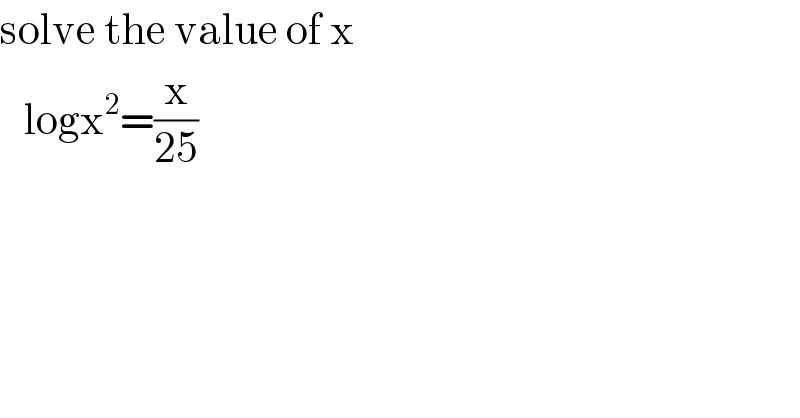
solve the value of x logx^2 =(x/(25))
$$\mathrm{solve}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x} \\ $$$$\:\:\:\mathrm{logx}^{\mathrm{2}} =\frac{\mathrm{x}}{\mathrm{25}} \\ $$
Answered by mrW1 last updated on 01/Feb/17
I. if x>0: log x^2 =(x/(25)) ⇒2log x=(x/(25)) log x=(x/(50)) ((ln x)/(ln 10))=(x/(50)) ln x=((ln 10)/(50))x=−ax with a=−((ln 10)/(50)) ln x=−ax x=e^(−ax) xe^(ax) =1 (ax)e^(ax) =a ⇒ax=W(a) Lambert W function ⇒x=((W(a))/a)=−((W(−((ln 10)/(50))))/((ln 10)/(50)))=−((W(−0.046052))/(0.046052)) { ((=((−0.048332)/(−0.046052))=1.049516)),((=((−4.605162)/(−0.046052))=100)) :} II. if x<0: log x^2 =(x/(25)) let t=−x, t>0 log (−t)^2 =−(t/(25)) log (t)^2 =−(t/(25)) 2log t=−(t/(25)) see above t=((W(((ln 10)/(50))))/((ln 10)/(50))) x=−t=−((W(((ln 10)/(50))))/((ln 10)/(50)))=−((W(0.046052))/(0.046052)) =−((0.044067)/(0.046052))=−0.956903 ⇒ x=−((W(±((ln 10)/(50))))/((ln 10)/(50)))≈ { ((−0.956903)),((1.049516)),((100)) :}
$${I}.\:{if}\:{x}>\mathrm{0}: \\ $$$$\mathrm{log}\:{x}^{\mathrm{2}} =\frac{{x}}{\mathrm{25}} \\ $$$$\Rightarrow\mathrm{2log}\:{x}=\frac{{x}}{\mathrm{25}} \\ $$$$\mathrm{log}\:{x}=\frac{{x}}{\mathrm{50}} \\ $$$$\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{10}}=\frac{{x}}{\mathrm{50}} \\ $$$$\mathrm{ln}\:{x}=\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}{x}=−{ax} \\ $$$${with}\:{a}=−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}} \\ $$$$\mathrm{ln}\:{x}=−{ax} \\ $$$${x}={e}^{−{ax}} \\ $$$${xe}^{{ax}} =\mathrm{1} \\ $$$$\left({ax}\right){e}^{{ax}} ={a} \\ $$$$\Rightarrow{ax}={W}\left({a}\right)\:\:\:\:{Lambert}\:{W}\:{function} \\ $$$$\Rightarrow{x}=\frac{{W}\left({a}\right)}{{a}}=−\frac{{W}\left(−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}\right)}{\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}}=−\frac{{W}\left(−\mathrm{0}.\mathrm{046052}\right)}{\mathrm{0}.\mathrm{046052}} \\ $$$$\begin{cases}{=\frac{−\mathrm{0}.\mathrm{048332}}{−\mathrm{0}.\mathrm{046052}}=\mathrm{1}.\mathrm{049516}}\\{=\frac{−\mathrm{4}.\mathrm{605162}}{−\mathrm{0}.\mathrm{046052}}=\mathrm{100}}\end{cases} \\ $$$$ \\ $$$${II}.\:{if}\:{x}<\mathrm{0}: \\ $$$$\mathrm{log}\:{x}^{\mathrm{2}} =\frac{{x}}{\mathrm{25}} \\ $$$${let}\:{t}=−{x},\:{t}>\mathrm{0} \\ $$$$\mathrm{log}\:\left(−{t}\right)^{\mathrm{2}} =−\frac{{t}}{\mathrm{25}} \\ $$$$\mathrm{log}\:\left({t}\right)^{\mathrm{2}} =−\frac{{t}}{\mathrm{25}} \\ $$$$\mathrm{2log}\:{t}=−\frac{{t}}{\mathrm{25}} \\ $$$${see}\:{above} \\ $$$${t}=\frac{{W}\left(\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}\right)}{\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}} \\ $$$${x}=−{t}=−\frac{{W}\left(\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}\right)}{\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}}=−\frac{{W}\left(\mathrm{0}.\mathrm{046052}\right)}{\mathrm{0}.\mathrm{046052}} \\ $$$$=−\frac{\mathrm{0}.\mathrm{044067}}{\mathrm{0}.\mathrm{046052}}=−\mathrm{0}.\mathrm{956903} \\ $$$$ \\ $$$$\Rightarrow\:{x}=−\frac{{W}\left(\pm\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}\right)}{\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}}\approx\begin{cases}{−\mathrm{0}.\mathrm{956903}}\\{\mathrm{1}.\mathrm{049516}}\\{\mathrm{100}}\end{cases} \\ $$
Answered by arge last updated on 04/Feb/17
2log x=(x/(25)) log x=y x=50y
$$\mathrm{2}{log}\:{x}=\frac{{x}}{\mathrm{25}} \\ $$$$ \\ $$$${log}\:{x}={y} \\ $$$$ \\ $$$${x}=\mathrm{50}{y} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *