Question Number 75721 by Gazella thomsonii last updated on 15/Dec/19
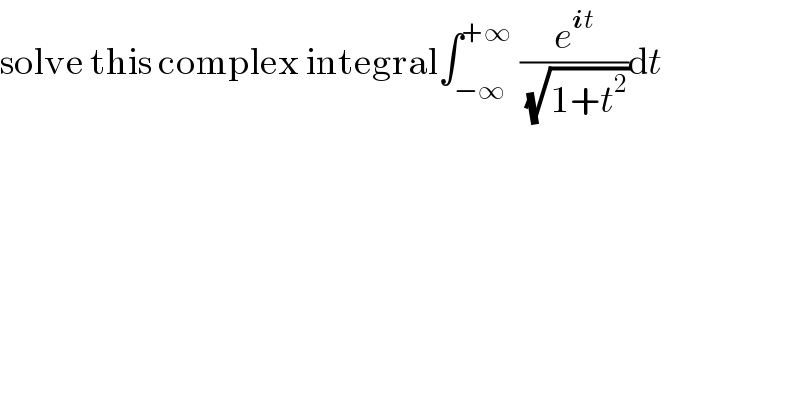
$$\mathrm{solve}\:\mathrm{this}\:\mathrm{complex}\:\mathrm{integral}\int_{−\infty} ^{+\infty} \:\frac{{e}^{\boldsymbol{{i}}{t}} }{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\mathrm{d}{t} \\ $$
Commented by MJS last updated on 15/Dec/19
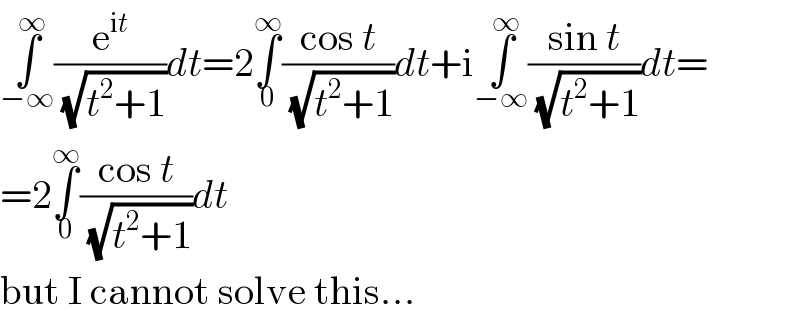
$$\underset{−\infty} {\overset{\infty} {\int}}\frac{\mathrm{e}^{\mathrm{i}{t}} }{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{dt}=\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{cos}\:{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{dt}+\mathrm{i}\underset{−\infty} {\overset{\infty} {\int}}\frac{\mathrm{sin}\:{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{dt}= \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{cos}\:{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{dt} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{cannot}\:\mathrm{solve}\:\mathrm{this}… \\ $$
